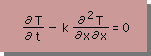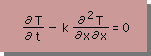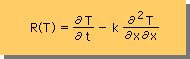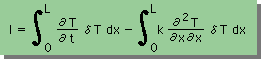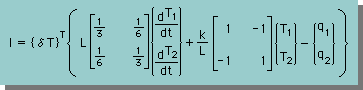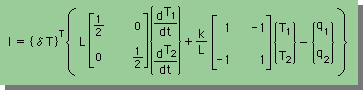Time Derivative and Upwind Method
Time Derivative Term
■1次元Heat Equation の有限要素式■
時間項の取り扱いについては、様々な方法が提案されています。どんな方法が有るかは、Referencesでチェックしてください。
ここでは、ごく一般的で且つ最も安定性の良い方法を紹介します。
まず、解く微分方程式を、下に表示します。
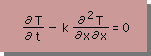 上式のResidual(残差)と積分式(有限要素式)は、次の様に定義されます。
上式のResidual(残差)と積分式(有限要素式)は、次の様に定義されます。
上の積分式を見ると、時間項を生成項として取り扱っていることに気付くと思います。
通常ですと、∬R(T)δTdxdt として計算を進めるところですが、ますます問題を難しくしてしまうので、ここでは使いません。
1次要素を用いて、上の積分式を計算すると、次のマトリックス型有限要素式が得られます。
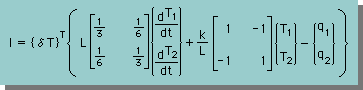 ここに、L=要素の長さを意味します。
上式の時間項のマトリックスをみて下さい。非対角要素に1/6があります。
これは、何を意味しているかと言うと、(1/6)dT1/dt の情報が直接dT2/dt に拡散していることになります。
つまり、T1とT2の2点間の距離に関係なく、T1とT2は情報のやりとりを行うことになります。
本来ですと、熱伝導係数(k)を通して拡散すべきであるのだが。
ここに、L=要素の長さを意味します。
上式の時間項のマトリックスをみて下さい。非対角要素に1/6があります。
これは、何を意味しているかと言うと、(1/6)dT1/dt の情報が直接dT2/dt に拡散していることになります。
つまり、T1とT2の2点間の距離に関係なく、T1とT2は情報のやりとりを行うことになります。
本来ですと、熱伝導係数(k)を通して拡散すべきであるのだが。
この矛盾を解決するために、Lumpingという手続きが提案されました。
Lumpingとは、マトリックスの非対角要素の全てをその行の対角要素に足し込むことをいいます。
| 時間項処理手続き その1 |
|---|
| 時間項のマトリックスには、Lumpingを施す。 |
上式の時間項のマトリックスをLumpingすると、次の様になります。
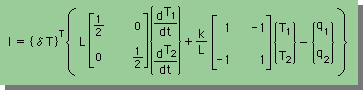
BACK to Solid Mechanics
NEXT
Menu
Heat Equation
Time derivative
Upwind
1 Dim Example