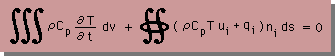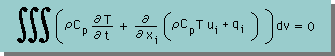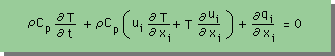
■3次元流体内の熱収支■
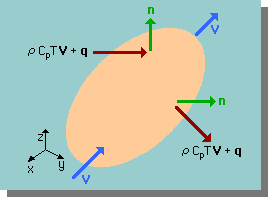
下図に示す楕円型の部分は、流体が存在している空間に設けた任意の3次元領域です。ここでは、この領域の境界と内部で何が起きているかについて勉強します。

図中の(ρC_pTV)は、流体の速度Vによって運ばれる熱です。qは、以前と同じで、拡散によって運ばれる熱です。つまり、ρC_pTV+qは、境界上でHeat flux になります。nは、境界面に対し垂直で外向きの単位ベクトルです。また、図中の座標系は、弾性解析のそれとは違って、observation coordinate sysytem になります。つまり、貴方は、領域の外に立って、任意の領域で何が起きているかを観察することになります。

上図をベースにして、Heat balance equation を書くと次の様になります。

以前紹介したDivergenceの定理をこの式の境界積分に適用すると、下式の様になります。貴方は、そうなることを確認して下さい。

積分の領域は、任意ですから積分される量もゼロになります。つまり、下式です。