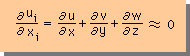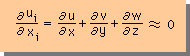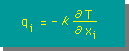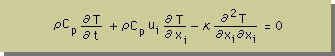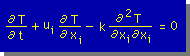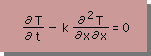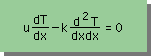Time Derivative and Upwind Method
Heat Equation-2
流体は、流れがスムーズであると、ほぼ非圧縮性の流れになります。もちろん、意図的に圧縮すれば別ですが。しかし、流体は完全な非圧縮性になることはありません。詳細は、流体力学のところで説明します。したがって、次のことが言えます。
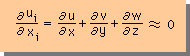 そして、流体内での拡散も固体内での拡散と同じ様に、次の式で表すことが出来ます。
そして、流体内での拡散も固体内での拡散と同じ様に、次の式で表すことが出来ます。
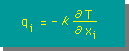 上の2つをHeat balance equation に代入すると、次の式が得られます。
上の2つをHeat balance equation に代入すると、次の式が得られます。
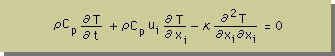 更に、式を簡略化するために、上式の両辺を ρCp で割ります。すると、式は次の様になります。
更に、式を簡略化するために、上式の両辺を ρCp で割ります。すると、式は次の様になります。
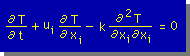 ここに、熱伝導係数(κ)をρCp で割った値を Thermal diffusivity といい、0℃の水の値は0.001339cm2/sec なることが知られています。
ここに、熱伝導係数(κ)をρCp で割った値を Thermal diffusivity といい、0℃の水の値は0.001339cm2/sec なることが知られています。
■1次元非定常熱拡散方程式■
時間項の勉強をするために、1次元非定常熱拡散方程式を取り上げます。つまり、上式の移流項を取り除き、1次元微分方程式にします。下式がそうです。
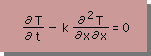 流体解析を行うと、必ずといっていいほど、時間項の取り扱いに悩ませられます。次のセックションで詳しく説明しますので、しっかり勉強して下さい。
流体解析を行うと、必ずといっていいほど、時間項の取り扱いに悩ませられます。次のセックションで詳しく説明しますので、しっかり勉強して下さい。
■1次元定常熱移流拡散方程式■
時間項よりもbehaviorが悪いのが、移流項です。移流項のうまい処理方法の考え方が、差分法の分野で紹介されました。ここでは、下式の1次元定常熱移流拡散方程式をベースに、その考え方を解読してみます。
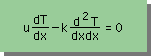
BACK
NEXT Time derivative
Menu
Heat Equation
Time derivative
Upwind
1 Dim Example