そもそも Reduced Integration Technique は、Shell要素のせん断応力の精度を向上させるために、Zienkiewicz によって開発されました。この Technique によって解析精度(変位と応力の関係)は、格段に良くなりました。しかし、衝突解析の様な時間依存の解析では、振動モードの違いにより、Hourglass 振動 が、解析結果に現れてきます。Hourglass 振動は、解析結果を低下させることになります。現在では、既にHourglass 振動を押さえる数値解析手法が開発されています。このTechnique について、もっと知りたい方は、最新の Zienkiewicz の本や論文を読んで下さいね。

さて、話を元に戻しましょう。プログラミングで注意してほしいことは、{u}^(t+Δt)が得られた後、圧力を得るためにdivVを計算する時にも、1ランク低い積分精度で計算する必要があります。

■平均圧力(p)の計算■
流体が動いているときの圧力を知る方法として、平均圧力があります。平均圧力は、x,y,z方向のnormal stressの平均を計算することで値が得られます。圧力の方向は、normal stressの方向の逆(180度)ですから、平均圧力は、下式の様になります。

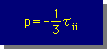
ここに、τ_ii=τ_xx+τ_yy+τ_zz です。
上式を展開して、アレンジすると、下式が得られます。

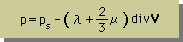
係数(λ+2/3μ)をbulk viscosity と言いますが、各流体について実際のbulk viscosityを測定したという報告は数える程です。理由は、Stokes condition により、λを測定する必要がなかったからです。この件については、後程、詳しく紹介します。それから、p_s は、hydrostaic pressure のことで、流体の流れの影響を受けないように測定した圧力です。Thermodynamic pressure とも言われます。実際、Pitot tube を使い圧力(p_s)を測定しようとすると、なんらかの流れの影響を受けてしまい、p_s でもない 平均圧力(p) でもない値が観測されることになります。

平均圧力(p)について、もうちょっと述べます。ここでの流体力学の支配方程式の展開において、第2粘性係数(λ)は、μよりも、かなり大きい値であると仮定していますから(λ＞＞μ)、上の平均圧力の式のμを無視することができます。つまり、下式の様になります。