■4節点1次要素内の平均divVの計算■
まず要素の面積計算Aですが、既に紹介しているように以下で計算できます。合計を示すΣが1から4になっているのは、要素が４つの境界線からできているからです。詳細についてはGreen's Theoremを見て下さい。

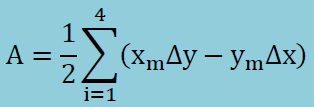
上式中の諸変数は、以下のように定義されています。以下のi+1が5の場合は、1とします。

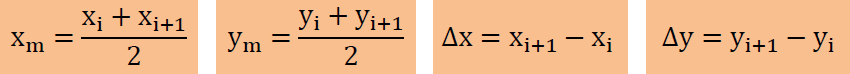
そして面積の式のxをuでyをvで置き換えると要素内の平均divVは以下で計算できます。

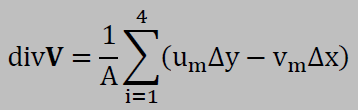
式中のu_mとv_mは以下のように定義してあります。つまり、境界線の中点での値ということです。

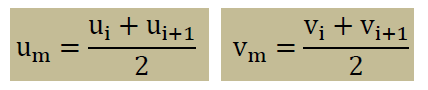
■8節点または9節点2次要素内の平均divVの計算■
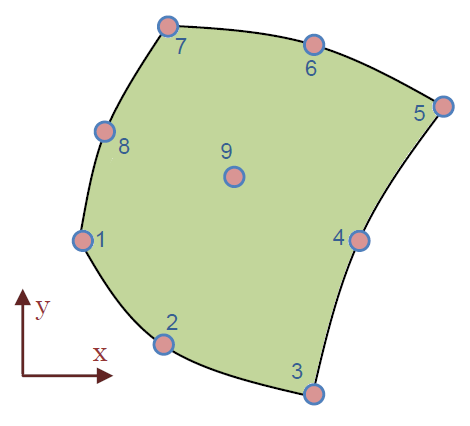
2次要素の場合は、ちょっと計算が複雑になりますが、1次要素のときと同じ手順で式に展開を行えば解を導くことができます。 まず、2次要素を下に示します。