計算を行うのは、下に示す2つの式の右辺です。 1次要素との違いは、要素の境界線のx, y, u, vが2次式になっているということです。
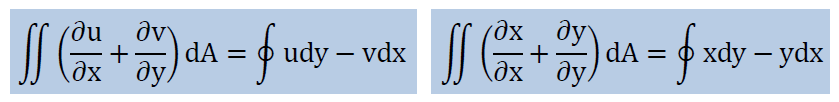
その2次式ですが、1次元の Parabolic Element で紹介した形状関数を使うと、下に示すようにx, y, u, vを無次元変数ξで書けます。説明のために下の式は上図の節点1から節点3までの区間です。
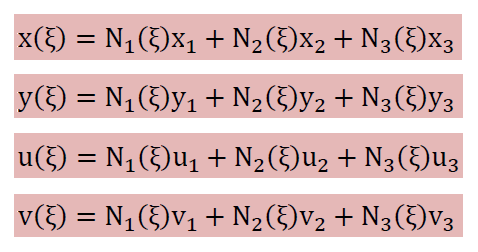
これらを発散の定理に代入すると面積Aと発散の積分は次のようになります。 下式のdivVは要素内の平均値を表しています。
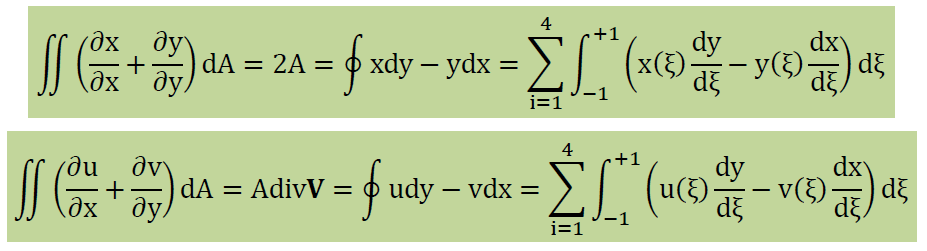
つまり以下で要素の面積Aと要素内の平均divVは計算できます。
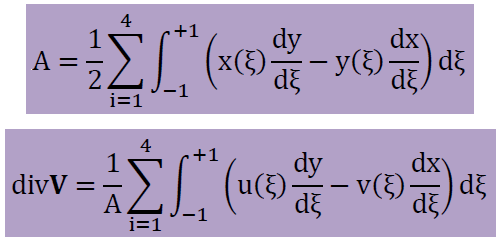
| BACK | NEXT |
|---|
| Menu | Govern | FEM | 2nd Visco | DCF | Cylinder | /Heat | Lub |