無次元座標によるxとyの微分は次に示すように形状関数を微分することにより得られます。
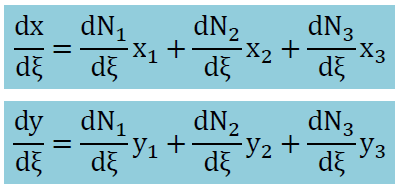
すると、x(dy/dξ)は以下のように書けます。
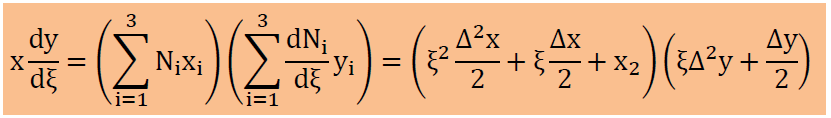
ここからは節点1から3までの境界線を取り上げて説明します。 その前に、上式中のΔx, Δy, Δ2x, Δ2yは、以下で計算しています。
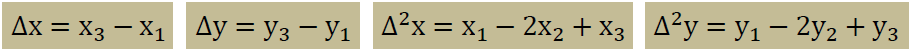
積分範囲が-1から+1までですので、積分される項がξの偶数指数のみが有限な積分結果になります。 結果的に境界積分は以下に示すよう式で与えられます。
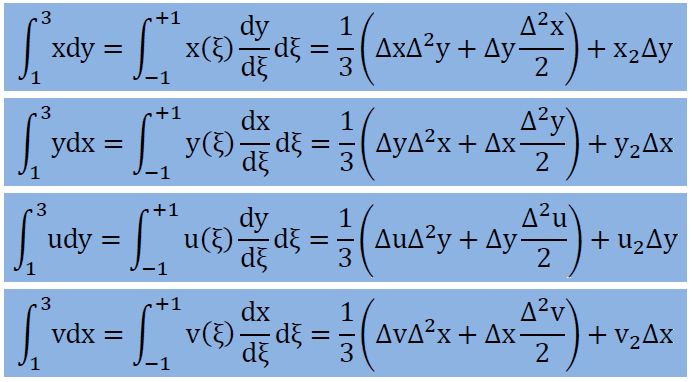
| BACK | NEXT |
|---|
| Menu | Govern | FEM | 2nd Visco | DCF | Cylinder | /Heat | Lub |