ここに、Δu, Δv, Δ²u, Δ²vは以下のように定義してあります。

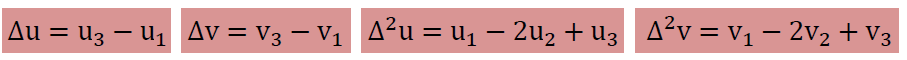
上の積分を残りの3つの境界線で行いお互いの合計を計算すると、面積AとAdivVが計算されることになります。 ここで紹介した計算方法は、グラフィックプログラムNSG4FILE.FORとNSG9FILE.FORでの圧力計算に使われています。

上で説明した1節点から3節点までの積分が正しいかどうかを確認するために、1節点から3節点までのセグメントを 複数個使って半径が1の円周を分割し円の面積を計算するプログラム CIRCLEAREA.FORを作成してみました。 面積はπですので計算された面積(A)からπを引き誤差を分割数の関数として検証してみました。結果は以下の 通りです。

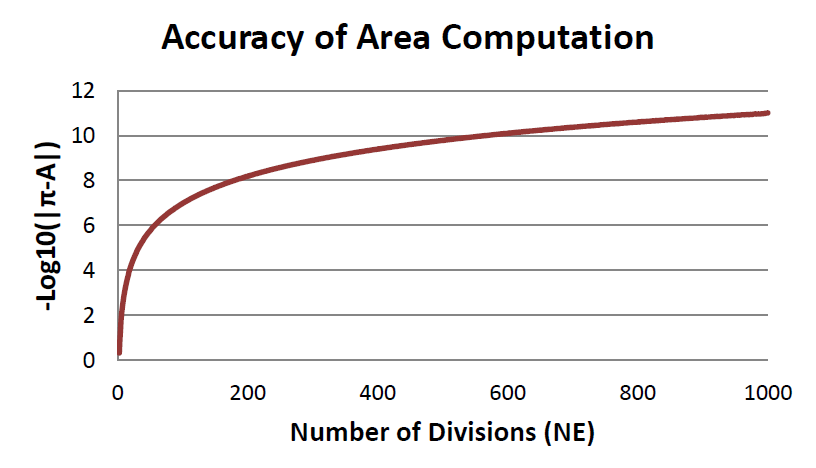
横軸は分割数のNEです。縦軸は、-log₁₀(|π-A|)で、何桁目までπと一致しているかを示します。 プログラムですが実はπを使って円を作っていますので、そのπの精度に計算(A)は左右されています。 計算結果をみると、2分割でA=2 2.6666666666666665、3分割でA=3.03108891324553、9分割でA=3.14006030537821、 1000分割でA=3.14159265357989になっています。1000分割では小数点11桁まで合っています。

これでDriven Cavity Flowの話は終わりです。次は円柱周りの流れ解析です。