■Stream Function の計算方法■
2次元の流れを可視化する方法で最も理解し易いのがStream Function(流れ関数)です。
速度ベクトルV=ui+vj が求まればStream Function を計算することが出来ます。
勿論、領域内の流体のマスバランスが満足されていないと計算はできません。
つまり、流入量と流出量が同じであるということです。
流入量がゼロで流出量がゼロの場合もStream Functionは計算できます。
流体力学の本を見るとStream Function(ψ) の定義は以下のように書かれています。
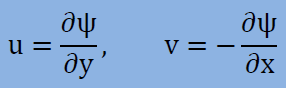
流れに渦があるかどうかは、速度ベクトルのサーキュレーションを計算すると判断がつきます。サーキュレーション curlV はz軸方向を示すベクトル量ですのでスカラーにするためz軸方向の単位ベクトルkを内積します。結果的に以下のようになります。
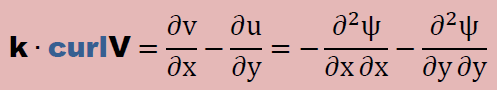
したがって、下式のPoisson's equation を境界条件で解析すると、Stream Function が得られます。
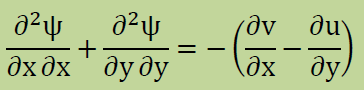
境界条件としてはDriven Cavity Flowの場合、まず流入量Qを計算します。 そして流入量と流出量の境界条件を∂ψ/∂n=0とします。 次に速度u=1の境界をψ=Qとし、残りの境界をψ=0とすればStream Functionが得られます。 詳しくはSET4NS12NEW.FORの B. C. FOR STREAM FUNCTIONを見て下さい。
■発散の定理を使ったdivVの計算方法■
流速ベクトルが計算されると要素毎にP=-λdivVで圧力を計算することができます。
それには、要素内の低減積分の積分点でdivV=∂u/∂x+∂v/∂yを計算する必要があります。
線形要素の場合は要素中心、2次要素の場合は4点でdivVを計算し平均をとります。
このような方法でdivVを計算すると演算数が多くなり、数点(線形要素の場合は1点)での計算で要素の平均を表すには、
少し煩雑な気がします。そこで積分点に左右されなくて計算量が少ない方法として発散の定理による計算方法があります。
それはこれまでの何回も本サイトで出てきている以下の式の右辺になります。
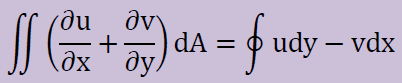
要素単位で上の式の右辺を計算し要素の面積で割れば要素内の平均のdivVが計算されます。
| BACK | NEXT |
|---|
| Menu | Govern | FEM | 2nd Visco | DCF | Cylinder | /Heat | Lub |