■計算例■
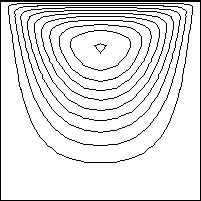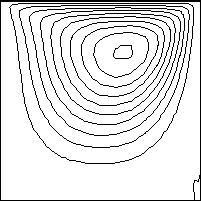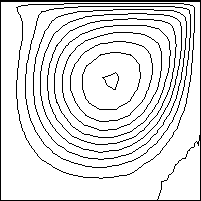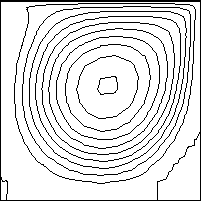
様々なReynolds 数のDriven-cavity flow をおみせします。下にアニメーションが表示されます。計算には、λ/μ=1x107 を使いました。そして、下表に示す17のReynolds 数を使っています。Reynolds 数が大きくなるにつれ、渦の中心が領域の中心に移動しているのが分かります。
| Reynolds number | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0001 | 20 | 40 | 60 | 80 | 100 | 150 | 200 | 250 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 999 |
■9節点2次要素の紹介とImplicit法のプログラム■
流体の計算で2次要素を使うのは適切ではないと思いますが、プログラムを9節点2次要素へアップグレードするのは、とても簡単ですので作成してみました。
やったことは、プログラムのSUBROUTINE ISOPARAに9節点2次要素の形状関数を書き込むだけです。後は、入力データを作成する
プログラムSET9NS12NEW.FORで
ND=9とINTEPT=3を指定する必要があります。実際に入力データを作成し解析プログラムNSEQ8DD.FORで計算を実行すると、タイムステップ(DT)がかなり小さくなり計算の進みが悪いです。多分、Crank-Nicolson法がネックになっていると思われます。そこで、計算をシンプルにするためにImplicit法による解析プログラム
NSEQ8DDXLLDECOMPOSITION-IMPLICIT.FORを作成しました。
Implicit法とは、時間項以外の未知数uとvはt+Δt時のみとする方法です。Crank-Nicolson法はt時とt+Δt時の平均をとっています。更に連立方程式の計算に[L][D][L]TDecompositionを採用しました。Convective項は、NSEQ8DD.FORと同様に繰り返し計算で整合性を取っています。
実際に計算を実行すると、多分9節点2次要素の場合NSEQ8DD.FORと比較すると、数百倍の速さになったと思います。4節点1次要素も使えるようにしてあります。1次要素の場合は、3倍程度の速さになっています。以下に、ここで使ったプログラムを紹介しておきます。
| プログラム名 | 要素 | 簡単な説明 |
|---|---|---|
| NSEQ8DD.FOR | 4節点1次と 9節点2次 |
Crank-Nicolson法2次元流体解析 |
| NSEQ8DDXLLDECOMPOSITION- IMPLICIT.FOR |
4節点1次と 9節点2次 |
Implicit法2次元流体解析 |
| SET4NS12NEW.FOR | 4節点1次 | Driven-Cavity Flowの入力データを作成 |
| SET9NS12NEW.FOR | 9節点2次 | Driven-Cavity Flowの入力データを作成 |
| NSG4FILE.FOR | 4節点1次 | グラフィックデータを計算 |
| NSG9FILE.FOR | 9節点2次 | グラフィックデータを計算 |
| BACK | NEXT |
|---|
| Menu | Govern | FEM | 2nd Visco | DCF | Cylinder | /Heat | Lub |