Calculus in Finite Element Method
Scalar and Vectors in 2dim and 3dim-3

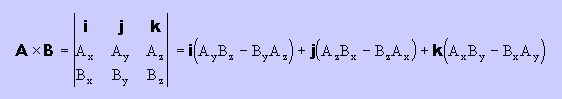
■Cross Product■

もう１つのベクトルのオペレーションに Cross Product があります。 電磁気学において、2つのベクトルの Cross Product は、物理的な意味をもっています。 例えば、磁場(B)の中を電荷(q)をもった物質が速度(V)で通過する時、物質に力(F)が働くことが知られています。 その力は、F=qVxBで与えられる。

Cross Product の計算方法ですが、次のmatrixのdeterminant で与えられています。 皆様も何処かで見たことはありますよね。

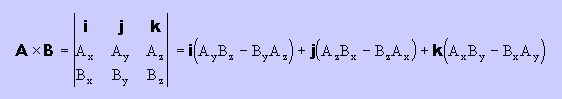
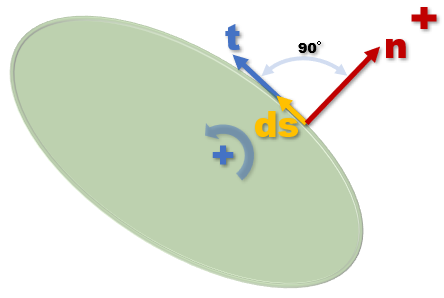
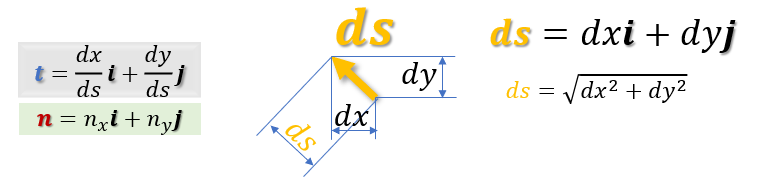
■2dim Unit Tangential and Normal Vectors■

2次元と3次元になると熱や流体の流れはベクトルで記述することになります。そこで重要になってくるのが下図に示す 単位接線ベクトル(Unit Tangential Vector)tと単位法線ベクトル(Unit Normal Vector)nです。 tは境界上の点の接線ベクトルで反時計方向がプラスです。 nはtに対し直角で境界に対し外向きがプラスです。

ベクトルdsは下図に示すように定義出来ます。 ですからtはdsをベクトル長dsで割ると得られます。

ではnはどのようにすれば得られるかです。tと90度の開きがあるので、 この事とベクトルのDot ProductとCross Productを使います。 次の図に示すようにn・t=0と n×t=1kになります。
BACK NEXT
Menu Fnc Drv Int(1) Dif Crd Chain Lhsptl Vec Green IndxN Int(2)