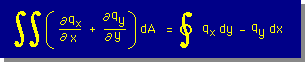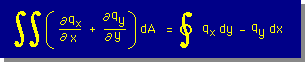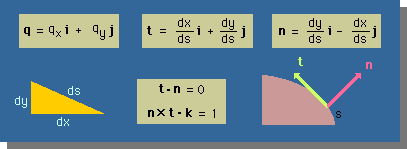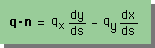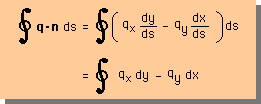Calculus in Finite Element Method
Green's Theorem-4
x方向とy方向の両方の積分結果が出たところで、2つを足し合わせます。
ここでは、積分領域を0からLxと0からLyに限定しましたが、積分領域は任意であっても、今まで学習したとこは、
使えることが知られています。すると、2つを足し合わせた結果は、下の左図の様になります。
また、線積分の方向と積分する部分は、右図のの様になります。
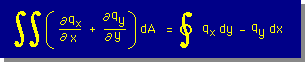
 これを、Greenの定理(Green's theorem)と言います。
勿論 Divergence の定理とも言います。というのも、左辺の領域積分が発散を意味しているからです。
"おー、教科書で見たことのある式だなー"とうなずく人は、多いと思います。
しかし、上の式がどの様に役立つかは書いてなかったと思います。ここでは、その辺をしっかりと勉強することにします。
これを、Greenの定理(Green's theorem)と言います。
勿論 Divergence の定理とも言います。というのも、左辺の領域積分が発散を意味しているからです。
"おー、教科書で見たことのある式だなー"とうなずく人は、多いと思います。
しかし、上の式がどの様に役立つかは書いてなかったと思います。ここでは、その辺をしっかりと勉強することにします。
ところで、突然ですが上式の右辺は、何者でしょう。
ここで、もう一度、基本的なベクトルについて復習します。
下に、ベクトル、q、t、nとそれらの特徴について書いて有りますので、十分理解しておいて下さい。
tは、unit tangential vectorで、nは、unit normal vectorです。
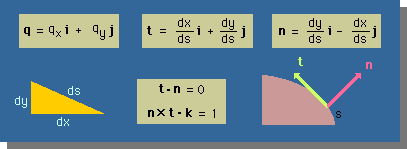 上のことがらを踏まえて、qとnの内積を計算してみて下さい。下図の様になりますよね。
上のことがらを踏まえて、qとnの内積を計算してみて下さい。下図の様になりますよね。
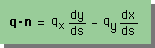 そして、上の式の両辺を、境界線(s)に沿って線積分すると、下の様になります。
そして、上の式の両辺を、境界線(s)に沿って線積分すると、下の様になります。
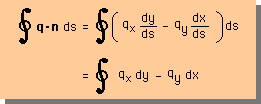
BACK
NEXT
Menu
Fnc
Drv
Int(1)
Dif
Crd
Chain
Lhsptl
Vec
Green
IndxN
Int(2)