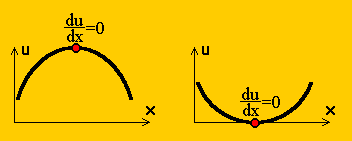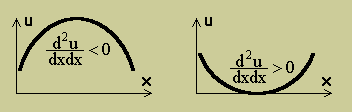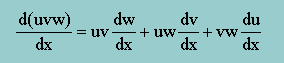
”本当にそーかな”と言う人は、u(x)=x², v(x)=x³ を使って確認してみて下さい。u(x)v(x)=x⁵ ですから注意して下さいね。 数学の歴史の本で見つけた話ですが、Bill Leibniz(1646-1716) は、長い間、上の式は間違いで、d(uv)/dx=udv/dx × vdu/dx が正しいと思っていたそうです。次元を調べれば、直にLeibnizの方が間違っていることに気付きますよね。Leibniz(ライプニッツ)は、数学の記号をつくる天才だったそうですよ。今、私達が使っている記号は、殆ど彼が作り上げたそうです。

応用として、3つの関数(u(x), v(x), w(x))の積の微分は、どうなるか考えてみましょう。これは、d(uvw)/dx=d(u(vw))/dx として考えれば簡単ですね。結果は、次の様になりますね。

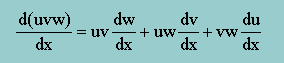
■Newton's 2nd Law■
弾性解析や流体解析の基本になっているのが、Newton's 2nd Lawです。FEMでは、質点でなく、領域にNewton's 2nd law を適用します。Newton's 2nd law とは、皆様が学校で教わった ΣF=ma です。ここに、Fは力、mは質量、aは加速度です。しかし、Isaac Newton(1642-1727) は、貴方が学校で習った式ではく、下の式を書いています。

確かに、殆どの場合、dm/dt=0 ですから ΣF=ma 良いのですが、Newtonは、もっと先(核分裂)を読んでいたのでしょうかね。ところで、Newton ですが、晩年は、大蔵大臣を勤めたとか。そう言えば、1ポンド札に彼が載っていますね。また、例の数学史の本ですが、Newtonは、服装に関しては、あまりセンスがなかった様ですよ。

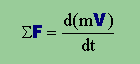
■最大最少■
数値計算では、極値(最大か最少)を計算することが多いです。下図に示す様に、関数の最大か最少は、関数の微分がゼロになる点で起きます。

数値計算で最大か最少を探す道具として、Newton-Raphson 法があります。この方法は、関数U(x)が ゼロ になる x を計算してくれます。このとき、最大か最少が存在している関数を u(x) とすると、U(x)=du(x)/dx になりますね。
関数u(x)が最大か最少になる点 x は、見つかりました。では、その点は、いったい最大なのか最少なのかを知りたくなりますね。それには、関数 u(x) の2階微分を計算しなくてはなりません。下図をみて下さい。

つまり、1階微分が位置 x でゼロになっていて、2階微分が負になっていると、関数u(x)は、x で最大になっていることが分かります。微分については、このくらい理解できればOKです。