ここに、[L]は下三角行列、[D]は対角行列を示します。[L]の対角要素は1になっています。 よって、次を計算することになります。このように分解できれば、後は代入のみで未知数{z}を得ることができます。

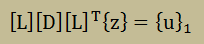
まず、新しい未知数{z’}を導入し、上式の左辺の一部を以下のように定義します。

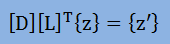
すると、未知数{z’}は以下で簡単に計算できます。

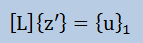
この時点では、z'_n=u_nですから次にz'_n-1が代入で計算できます。 このように、次から次えと計算をすれば、全ての{z'}が計算できます。 次に以下のように置きます。

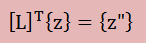
すると、[D][L]^T{z}={z'}から、以下の{z"}が計算できます。

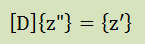
最後に、次の式から{z}が計算されます。

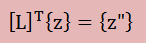
以上をまとめると{x}=[]^-1{u}₁ の計算手順は、以下のようになります。

⇒ ⇒

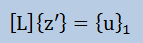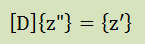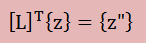
{z}が計算されれば、α₁は、α₁={z}^T{u}₁で計算できます

以降は、以前説明したLanczos法を参考にして下さい。このように行列の分解法を用いると、 []{z}={u}₂や []{z}={u}₃ やそれ以降の計算が高速に実行できます。しかし、行列の分解には多少の時間がかかります。 ここで、例題を計算しておきます。上で用いた10×10の行列を用いて固有値を計算してみましょう。 プログラムですが、 [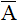]{z}={u}₁ で計算する方法(つまり行列をLU分解しな方法)がLANCZOSPRINCIPLE5.FORです。 そして、LU分解する方法がLANCZOSPRINCIPLE6.FORです。