ここで、注目したいのは、部分空間の固有値は元の空間の近似ですから計算された固有値は元の空間の 固有値でもあるということになります。とは言っても問題になるのが、元の空間での固有値の精度です。 そのためには、やはり以下で誤差判定しなければなりません。

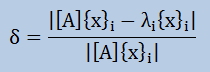
弾性解析の場合は、以下の式を判定に使うことになります。

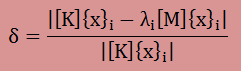
例えば、δが0.001以下は合格、それ以上は不合格とするとか。

■Lanczos法と近似計算の組み合わせ■
Galerkinの方法に従いm＜nを使って、以前に説明したLanczos法で三角対角行列 [T] を作成してみましょう (Shift-Invert Lanczos法は後で説明)。 そして固有値を計算し、真値との差を確認しておきます。計算手順としては、まずαとβを計算し、 サイズがn×mの[U]行列とサイズがm×mの[T]行列を生成します。その前に計算結果の検証をするために、 以下の行列をこれまでに紹介してきた方法で固有値の厳密解を出しておきましょう。

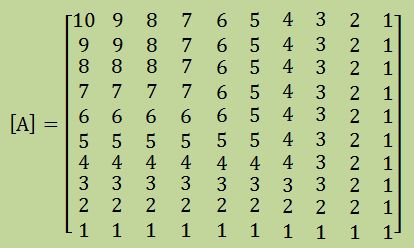
この行列の固有値の"厳密解"は、以下です。Bisection, Jacobi, Power法で計算し、誤差による多少の違いはありますが、 全てが同じ値であることを確認しました。 固有値は、プログラムLANCZOS_PRINCIPLE2.FORで計算しました。 LANCZOS_PRINCIPLE1.FORとの 違いはマトリクス[A]の生成部分と{u}₁の生成のみです。{u}₁は[A]の対角要素を用い、ベクトルの 長さが1に生成されるようになっています。