■固有値の近似解法■
ここからが本題です。これまでは、対象としている行列[A]がn×nのサイズの場合、 n個の固有値を計算する方法を紹介してきました。つまり、厳密的に固有値を求める方法を学んできました。 勿論、固有値を計算する過程で繰り返し計算を使いましたが、 これらの方法は無限回の繰り返しを行えば厳密解に収束することが知られています。

では、固有値の近似解法とはどんなことを指すのでしょう。行列[A]がn×nのサイズで、 得られる固有値の数がmの場合を指します。ここに、m＜＜nです。えー！と思いますが、 このような考えが生まれたことにより、固有値計算の能力が飛躍的に進展しました。 設計で欲しい範囲の周波数を与えると、その範囲にある固有値を計算してくれます。 このような考えの固有値の近似解法を持つのがGalerkin法です。 この方法と前に説明したLanczos法を融合したのが一般によく使われているShift-Invert Lanczos法です。 まずGalerkin法から説明します。

■Galerkin法■
サイズがn×nの行列[A]の固有値問題[A]{x}=λ{x}をm(m＜＜n)個のベクトル群からなる部分空間[Um]=[{u}1, {u}2,…,{u}m] に射影すると、部分空間内での固有値の近似解を得ることができます。 ベクトル群[U_m]=[{u}₁, {u}₂,…,{u}_m]は、正規直交になっていると仮定します。 これまでの話では、ベクトル群[U_n]=[{u}₁, {u}₂,…,{u}_n]でした。 ですから、[U_n]はn×nの行列でした。ここでの話は、各々の{u}がn次元ベクトルで数がm個ですから、[U_m]はn×mの行列になってしまいます。Galerkin法によれば、{x}=[U_m]{y}で置き換えても(射影しても)以下が成り立つと言っています。{y}は部分空間での固有ベクトルです。

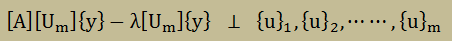
つまり、上式の左辺と右辺が直交していることになります。ですから、左辺に前から{u}_i^Tを掛け算すれば、左辺は以下になることになります。注意：[U_m]^T[U_m]=[I]_mXm

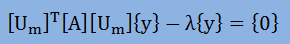
また、[T]=[U_m]^T[A][U_m]と置くと、上式は以下のようにも書けます。

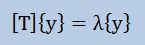
ここに、[T]はm×m, {y}はm次元になっています。 よって、上式から固有値λと固有ベクトル{y}を計算できれば、[A]の固有値問題を近似的に解いたことになります。 固有ベクトル{y}が計算できれば、元の空間の固有ベクトル{x}は、{x}=[U_m}{y}で計算できることになります。 [A]が10000000×10000000のサイズの行列であっても、 [T]を50×50のサイズにすれば、固有値λと固有ベクトル{y}は、 これまでに紹介してきた方法で簡単に計算することができます。どの方法も問題なく使えます。