Bisection法は、常に50回ほどの繰り返し計算が必要なのに対し、Newton- Raphson法を併用した方法では、20回以下の繰り返し計算で目的の精度に達しています。マトリクス[T]の固有値の計算時間が約半分になります。 しかし、P_n(λ)がアンダーフローに至るとBisection法のみで計算が進行されます。また、Newton-Raphson法に適した条件で固有値の計算をっ進めるためには、ある程度の精度が確保されるまでBisection法を用いるのが適切と考えます。そこで、 LANCZOS_PRINCIPLE7_WITH_NEWTON.FORでは、EPSBIという変数名を導入し、固有値の精度がEPSBIまで到達したらNewton-Raphson法へ進んでよいという許可を与えることにしました。これにより計算はいかなる時でも安定すると思います。

■固有ベクトルの計算■
Bisection法で固有値が計算された後、必要に応じて固有ベクトルを計算しなければなりません。 固有ベクトルを得るには、[T]{q}=λ{q}の連立方程式を未知数{q}について解かなければなりません。 しかし、これは[[T]‐λ[I]]{q}= {0}のように不定の連立方程式を解くことになり、 結局解の数はたくさん存在することになります。ではどうするか？。このような場合、 原点移動付逆ベキ乗法(Shifted Inverse Power Method)を用いて固有ベクトルを計算する方法があります。 ここでは、その計算方法を紹介します。
行列[T]が固有値λ_iとその固有ベクトル{q}_iが存在するとします。 すると[T]から−λ_i[I]を差し引いた行列[[T]−λ_i[I]]の固有値は0になりますが、 固有ベクトルについては何も変えていないので{q}_iに収束することになります。 しかし、このままでは式の展開が出来ないので、固有値λ_iに以下のような細工をします。

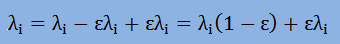
ここに、εは非常に小さな値としておきます。つまり、ε=0でλ_iは何も起きなかったことになります。
上式の固有値λ_iを式[T] {q}_i=λ_i{q}_iに代入すると以下のような展開になります。

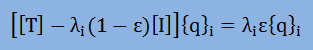
少しアレンジすると、

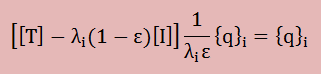
逆行列で表すと、

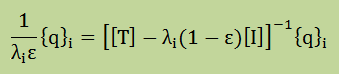
のように書けます。