■Bisection/Newton-Raphson法■
Bisection法の収束速度は、計算される固有値の上限と下限の平均をとっているため収束が非常に遅い。固有値が確実に計算されるという保障はありますが、低速の収束は、この方法の欠点と言えるでしょう。 そこで、収束の速いNewton-Raphson法を併用してみることにしてみました。最初はBisection法で固有値が存在する範囲を探り、範囲が定まったところでNewton-Raphson法を使って収束の高速化を図るという手法です。 手順としては、まず、固有値λの上限λ_upperと下限λ_lowerのP(λ_Bisection)の符号反転回数差が1になるまでBisection法を使います。次にNewton-Raphson法でより真に近い固有値λ_Newtonを以下で予測します。

このλ_Newtonが上限λ_upperと下限λ_lowerとの間にあれば新しいλとしてλ_Newtonを使い、そうでなければBisection法のλ_Bisectionを使い計算を進めます。そして、Bisection法に従い上限λ_upperと下限λ_lowerを更新します。P_n(λ)の微分のdP_n(λ)/dλは、上限値と下限値のP_n(λ)を使って計算します。ですから、上限値と下限値の差が狭くならないとdP_n(λ)/dλの精度は上がりません。 上限λ_upperと下限λ_lowerが十分に狭くなるとNewton-Raphson法が効果を発揮するようになり、収束速度は急激に速くなります。下図を見て下さい。例題として後で紹介する10×10の[A]で収束速度を調べてみました。

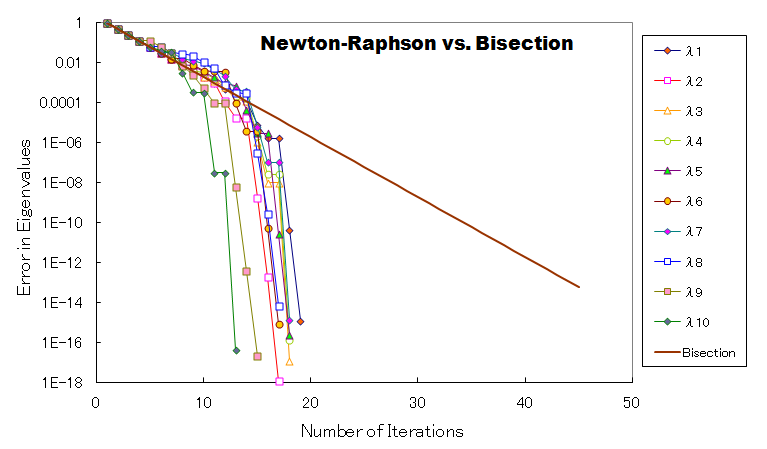
プログラムLANCZOS_PRINCIPLE_BASIC3.FORにNewton-Raphson法を取り込んだBisection法を紹介しています。見て下さい。Bisection法のサブプログラムが前よりちょっと長くなっています。微分のdP_n(λ)/dλをどのように計算しているか見て下さい。