自由端では、下図のように力を与えています。上側に−1000N/m、下側に+1000N/mが与えられています。

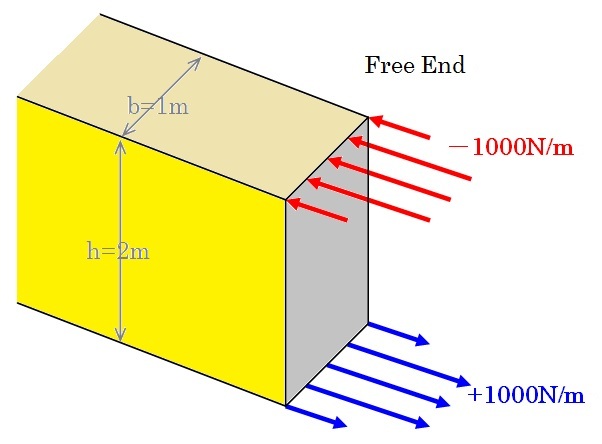
この問題の厳密解は、ビーム座標の原点の上面または下面での応力がτ_xx=3000Paになります。 M=2*1000[N/m]*(2[m]/2)*1[m]=2000Nm, 断面係数W=bh²/6=0.666666m³ですから応力は τ_xx=M/W=3000Paになります。ビーム中立軸の変位は、 Poisson比が影響しないためR=23000mの円弧で表されることになります。詳細は、2次元の計算例を見て下さい。 E=69*10⁶ Pa, I=bh³/12=0.666666m⁴ですからR=EI/M=23000mになります。

要素分割ですが、x方向がNEX、y方向がNEY、z方向がNEZで表します。 また、上で説明した収束解(27節点要素、NEX=100, NEY=4, NEZ=8)では、τxx=3000Pa, R=22997.376mになりました。 ということで、R=22997.376mを収束解としてこれから紹介する計算結果を評価します。

■8節点ヘキサ1次要素と27節点ヘキサ2次要素のよる結果■
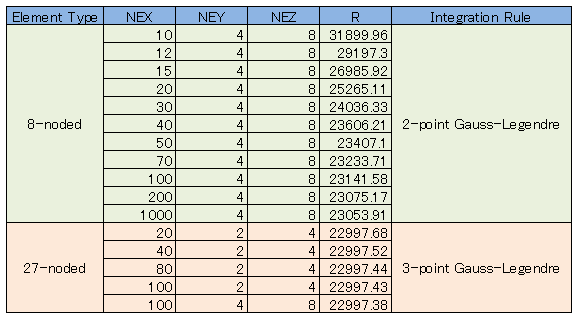
要素分割のNEX=100, NEY=4, NEZ=8で計算を実行すると、R=23141.58mになります。 このとき、積分はξ= 0.577350のGauss-Legendre 2点法を使っています。 X軸方向の要素分割数((NEX)を10から1000までふって計算すると、以下が得られます。NEYとNEZはそれぞれ4と8に 固定してあります。27-nodeでの計算結果も一緒に添えて置きました。