■ビームの自由端にモーメントMが作用している場合■
2次元と同じ問題を取り上げました。ただ違うのは、2次元の場合、平面歪を仮定した材料定数マトリクス[D]を使いましたが、 3次元の場合、平面歪/平面応力と言った仕分けがありません。しかし、どちらかと言うと3次元の計算結果には、 平面応力の影響が出やすくなります。 ここでは、27節点の要素を使いNEX=100, NEY=4, NEZ=8で下図に示すビームを分割した計算結果を収束解として話を進めます。

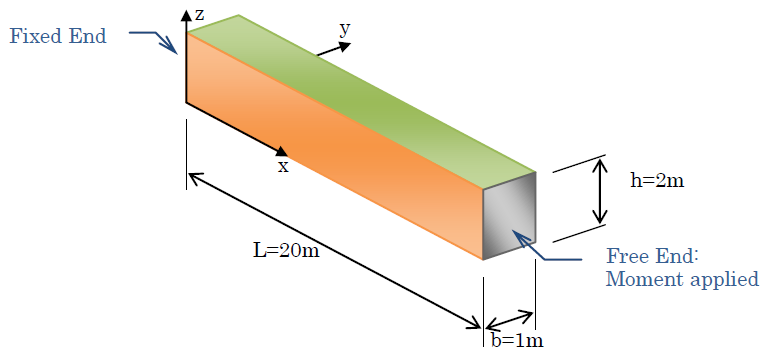
拘束端の境界条件ですが、ｘ方向は全ての節点でu=0を与えています。その他の方向は、以下のように拘束してあります。

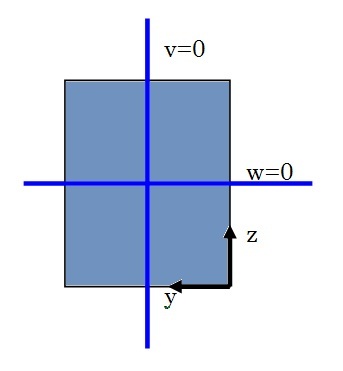
2つの線が交わる節点では、u, v, wの全てが拘束されていることになります。このような境界条件を与えた理由として、元々の問題は40mビームの両端にモーメントが与えられていました。そのビーム中間点の断面の中心は、完全に拘束されていていますが、その面のその他の点は面方向に自由に動くことができます。それを模擬すると、上の拘束条件になります