さらに、左辺を整理すると、下の連立方程式が出来上がります。
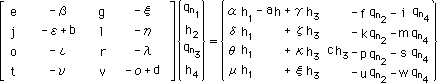
|
上の連立方程式 [A]{X}={RHS} を解くと、未知の変数が計算されます。
■直接 [A]{X}={RHS}を導く■
問題は、上の式に到達する過程で、[C]{h}+[G]{qn}-[F]{h}={0} の
| マトリックス[C],[G],[F]を計算機のメモリーに保存する必要があるか? |
下に、4要素の例題の場合の、 [A]{X}={RHS} の作成手順を下表に示します。貴方も、1行づつ確認して下さい。まず、Source point が、要素1にある場合です。計算されたCは、h1と掛算されRHS1へ加算されています。この辺を注意して下の表を観察して下さい。
| Source point |
要素番号 | G | F | C | RHS |
|---|---|---|---|---|---|
| 1 | 1 | A11=G | C=F | RHS1=F h1 | |
| 1 | 2 | A12=-F | C=C+F | RHS1=RHS1 - G*qn2 | |
| 1 | 3 | A13=G | C=C+F | RHS1=RHS1 + F*h3 | |
| 1 | 4 | A14=-F | C=C+F | RHS1=RHS1 - G*qn4 | |
| 1 | RHS1=RHS1 - C*h1 |
| BACK | NEXT |
|---|
| Menu | Fundamentals | Formulation | discretizatione | Example | Straight | Multi-D |