運動量の保存の式のMass Balanceの項を =0 と置くことは、運動量の保存の式から計算される速度ベクトル(u, v, w)は、質量の収支が満足されていることになります。つまり、下式は、Mass Balance がとれている運動量の保存の式、または、運動方程式ということになります。
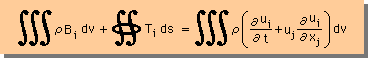
上式は、既にMass Balance(または連続の式)を満足していますので、Mass Balance式を連立に解く必要のないことが、理解できると思います。したがって、Navier-Stokes の式を解くときに連続の式が必要になることは、何かNavier-Stokes の式に不都合が有ることを示唆しています。
■流体がもたらす力■
流体が静止または流れているときは、流体の粒子間や流体と境界との間に、様々な力が発生しています。次にそれらの力について簡単に説明します。詳細については、流体の本を参考にして下さい。
(1)流れそのものによる力
下図の左に示す、運動量(Momentum)の保存による力のバランスです。運動量の保存を使って、下図の右のジェット流が壁にぶつかったときの、壁が支えなくてはならない力(Fx)を計算することが出来ます。
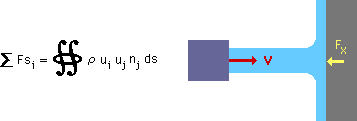
ジェットの噴射方向をxとし、ジェット流速と流量をそれぞれVとQとすると、ジェット方向に支えなくてはならない壁の力は、左図の式を計算すると、Fx=ρQVになります。貴方も計算してみて下さい。
(2)流体の粘性(μ)による力
下図に示す様に、流れに板を置いたときに発生する力をいいます。この力は、弾性解析のせん断応力に近い性質をもっています。粘性(μ)と応力については、後程詳しく説明します。
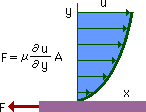
| BACK | NEXT |
|---|
| Menu | Govern | FEM | 2nd Visco | DCF | Cylinder | /Heat | Lub |