(3)圧力
圧力の表示には、静圧(Ps)と流体が動いているときに発生する平均圧(P)の2つが有ります。静圧は、流速による圧力成分を取り除いた圧力です。平均圧は、静圧と流速による圧力成分の和になっています。通常、圧力は、Pitot tube で測定できます。しかし、この測定された圧力は、静圧でもなく平均圧でもない、中間的存在です。後程、詳細に説明します。
(4)Body Forcesによる力
重力加速度や電磁誘導等、領域内の単位体積当たりに作用する外力による力を言います。流体が静止している状態は、重力加速度と水圧がバランスしているときです。そのバランスが崩れると、流体に動きが発生することになります。
(5)発散による力
流体の流れの方向が変わる時、流体に発散と収縮が起きます。発散と収縮の度合は、非常に小さいが、圧力に大きな影響を与えます。発散と収縮の代表的な例が、音(つまり圧力)の伝播です。音の伝播は、通常、私達が非圧縮性流体として取り扱っている水の中でも存在します。ここで紹介する流体力学では、流体の発散と収縮が大きな部分を占めています。
■流体の応力■
流体解析でも、弾性解析同様、Surface tractions, Ti を表す応力の式が、必要になります。
弾性解析の応力の式では、部材の変形と膨張/収縮が再現出来るようになっていましたね。
流体では、上で説明した圧力が弾性解析の応力の式に追加されます。ただし、変位は流速、Young係数とPoisson比は2種類の粘性係数で置き換えられます。つまり、流体の粘性(μ)による力と発散による力は、弾性解析と流体解析の間で、密接な関係があることになります。これらの関係を忠実に表しているのが、下に示すPoisson による流体の応力の式です。
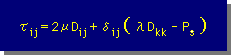
| 記号 | 名称 | 単位 | 代表値(H2O at 25'C) または式 |
|---|---|---|---|
| τij | 応力 | N/m2 | ---- |
| μ | 粘性係数 | N.sec/m2 | 0.89x10-3 |
| λ | 第2粘性係数 | N.sec/m2 | ? |
| Ps | 静圧 | N/m2 | γh |
| γ | Specific weight | N/m3 | ρg=9777.0 |
| ρ | 密度 | Kg/m3 | 997.0 |
| Dij | Rate of deformation tensor | sec-1 | 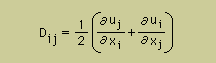 |
| Dkk | Divergence of V | sec-1 | 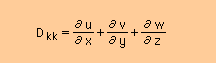 |
| BACK | NEXT |
|---|
| Menu | Govern | FEM | 2nd Visco | DCF | Cylinder | /Heat | Lub |