上式の右辺について、もうちょっと詳しく調べてみましょう。Mass Balance 式を導いたときを思い出して下さい。流体の質量、つまりρ・体積の収支を取り扱いましたよね。今度は、運動量ですから、ρU_i・体積の収支を考えることになります。したがって、dmU_i/dt は、次の様になります。

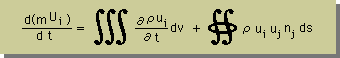
上式にの境界積分項は、u_iによって、ρu_iが運ばれることを意味しています。

さらに、Body forces と Surface tractions は、下に示す様に、表示的には、弾性解析のそれらとほぼ同じになります。勿論、積分される中味は違いますけどね。

これまでの結果を1つの式にまとめると、流体の運動量の保存の式は、次の様になります。

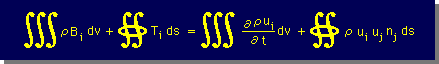
上式の右辺について、調べてみましょう。領域積分の項は、2つの関数の積の微分より、2つの項の和に分解できます。境界積分の項は、Divergenceの定理を用いて、領域積分に変換できます。したがって、上式の右辺は、下図に示す式になります。

上式を観察すると、Mass Balance 式が含まれていることに気付くと思います。d(mU_i)/dt から、Mass Balance 式が現われてくるのは、当り前なことですが。

余談ですが、Newton に関する歴史書にも、Newton's 2nd law とMass Balance 式について書かれているのを見たことがあります。それによると、『Newton は、なぜ F=ma と書かず、F=d(mV)/dt としたか』とあります。つまり、d(mV)/dt=ma+Vdm/dt であり、Newton は、dm/dt=0 としなかったのです。しかし、核分裂と核融合を除き、全ての物質の質量は保存されることが知られています。したがって、殆どのケースで、Mass Balance 式=0は、正しいと言えます。