流体力学では、しばしば、下に示す様な、領域内を移動する量の全微分が支配方程式に使われます。

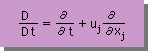
上式を用いて、Mass Balance 式を表すと、次の様になります。

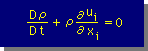
さらに、流体を圧縮可能な弾性体(弾性係数=K)とすると、Dρ/Dt=(ρ/K)Dp/Dtから、連続の式は次の様になります。

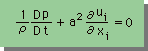
p=流体が受ける圧力、a=圧力の伝播する速度です。

ここで注意したいことは、流体の密度が時間および場所的に、あまり変化しないという仮定を取り入れると、上式は、divV=0 になります。つまり、これが非圧縮性流体の連続の式です。しかし、この連続の式、または上のMass Balance 式は、流体の状況を表しているだけで、連続体である流体の流れを支配する式ではない、と言うことを理解して下さい。言い替えると、『もし流体が、ほぼ非圧縮性であれば、流れの状態は、divV=0 になるでしょう』と言うことを上式は言っています。流体が非圧縮性であるかどうかは、あくまでも、流体内で起きている力のバランスの式(構成式)が、決めることですからね。

『では、なぜ、ここでMass Balance 式を紹介したのですか』と言う質問が出てくると思います。理由は、この後で紹介する運動量の保存の式の展開で、上のMass Balance 式を使うからです。

■運動量の保存の式 (Momentum Equation)■
運動量とは、流体の質量x流体の速度です。したがって、運動量の保存とは、流体の速度によって領域に運び込まれる運動量の収支のことを言います。つまり、下式に示す、Newton の第2の法則のことです。

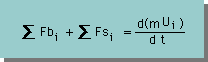
ここに、Fb_iは、重力等によるBody forces のことです。Fs_iは、領域の境界に作用しているSurface tractions を示しています。mは、領域内の流体の質量、U_iは、平均流速を意味します。