■Velocity Series■
ここでは、第2粘性係数の特徴および役割を、ちょっと違った角度から引き出すことにします。まず、速度ベクトルは、第2粘性係数が大きくなるにつれ、ある値に収束するものとします。このことより、次の速度ベクトルのシリーズが考えられます。

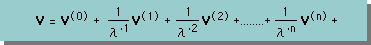
ここに、λ'=λ/λ₀。λ₀は、基準になる第2粘性係数のことですので、例えば、λ₀=1cm²/sec としても差し支え有りません。 第2粘性係数が無限大の場合、つまり非圧縮性流体を考慮すると、速度ベクトルは、V=V⁽⁰⁾ になることに注目して下さい。

次に、上式のDivergence を計算すると、下の様になります。

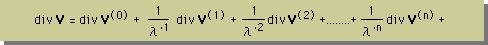
さらに、divV にλを乗ずると、下式になります。ここは、第2粘性係数で重要な箇所ですので、貴方もここの部分は、十分注意して勉強を進めて下さい。

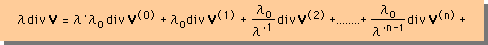
この時点で、私達が期待することは、上のλdivV を流体のmomentum equation へ代入し、λを無限大にした場合、divV=0 とλdivV=divV⁽¹⁾≠0 になることです。 つまり、divVとλとの間には、次の関係が考えられます。

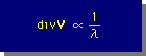
そして、上の関係が正しい場合、下図に示す様な結果が、期待できそうです。

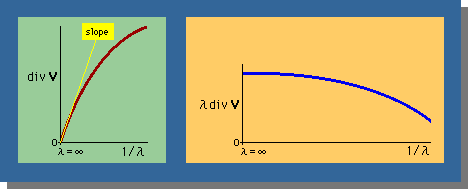
左図のslope は、λ＝∞付近での1/λに対するdivVの傾きを示します。そして、このslopeは、λdivVです。貴方もそうなることを、確認して下さい。