では、早速、上式のλdivVを流体のmomentum equation 代入してみましょう。結果は、無限に長い式になりますので、λ'ⁿ 項毎にまとめてみました。たとえば、λ'^-1 の項は、O(λ'^-1): の右に記述してあります。

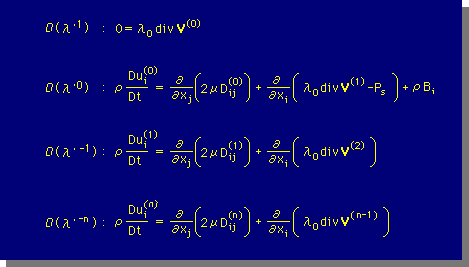
結果を観察してみましょう。まず、一番上の式ですが、divV⁽⁰⁾=0であることを意味しています。ここで、Velocity series を思い出してもらいたいのですが、V⁽⁰⁾ は、λ＝∞のときにVでした。よって、一番上の式は、momentum equation の中のλを∞にすると、divV=0に成ること伝えています。

次に2番目の式ですが、これは、λ＝∞のときのmomentum equation になります。理由は、λ＝∞のときV＝V⁽⁰⁾であり、divV⁽⁰⁾=0であるから、λ₀divV⁽¹⁾＝λdivVになるからです。参考までに、Navier-Stokes の式では、P_s-λdivVを平均圧力(P)で表しています。つまり、このことからも、λdivVは、有限な値を持つことになります。

3番目と4番目の式は、λ＝∞のとき消えますので、議論する必要はありませんね。

以上の観察から次のことが言えます。Velosity series とmomentum equation の組み合わせにおいて、第2粘性係数は、期待通りの特性があることが示されたことになります。次に行わなければならない作業は、Velosity series が論理上妥当であるかどうかをチェックすることです。つまり、第2粘性係数が大きくなるにつれ、Vが収束するかです。

Velosity series の論理上の妥当性のチェックに、数学的処理を行うことは難しいので、ここでは数値解析で妥当性のチェックを行うことにします。
ここで紹介している内容については、References の文献を参考にして下さい。もし、この件に関する文献の入手が困難な方へは、私へ連絡下さい。