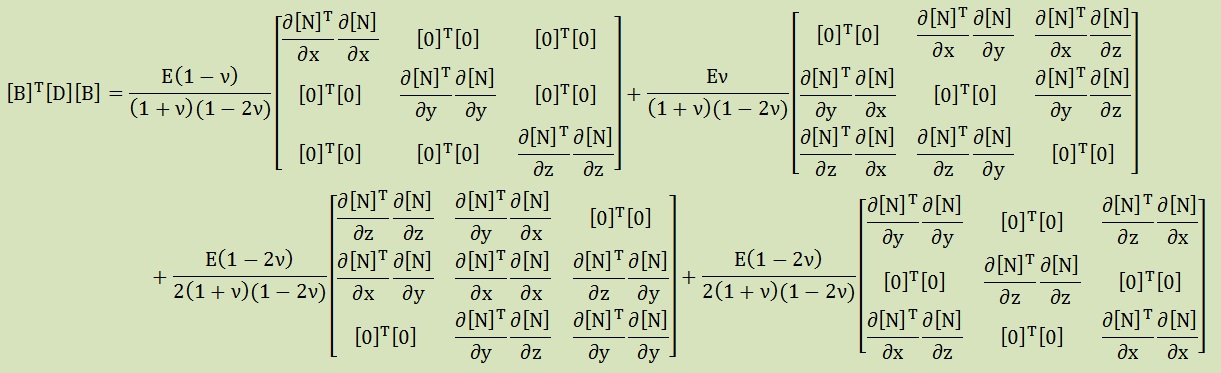
ここで、G=E/(2(1+ν))とλ=Eν/((1+ν)(1-2ν))の物性値を使うと、[B]T[D][B]は最終的に次のように書けます。Gは垂直応力およびせん断応力に関係し、λは膨張収縮応力に関係する物性値です。ポワソン比が0.5になると、λは無限大になります。つまり、Gとλはまったっく違った性質を持つ物性値ということになり、G項の積分とλ項の積分は違ったルールで行う必要がありそうです。 もう少し詳しく説明すると、右辺の第1の2G項は垂直応力、第2のλ項は膨張収縮、そして第3と4のG項がせん断応力の項に該当します。したがって、せん断応力部分低減精度積分法の場合は、第3と4のG項のみを低減精度で積分します。参考までに、流体解析では、圧力に密接に関係している第2のλ項を低減精度で積分します。しかし、市販ソフトで使われている低減精度積分を行うと自由度が1つ多くなり、アワーグラスと言う振動モードが発生します。このサイトでは、2次元のところでアワーグラスをまったく発生させない全ての項に適用させた低減精度積分を紹介しました。3次元でもこの低減精度積分を用いた計算結果を紹介します。 上の式を観察すると、以下を前もって計算しておくと便利であることが分かります。
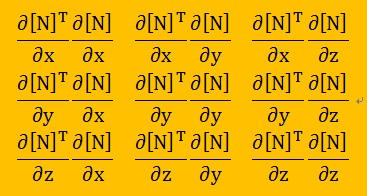
プログラムでは、要素毎にJacobianマトリクスとGauss-Legendre Quadratureを使って以下の積分を実施しておきます。
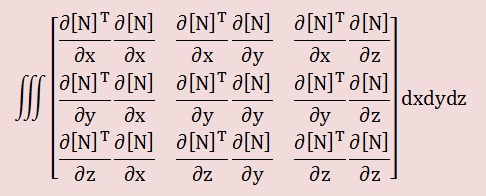
上の計算ですが、プログラムでは、以下のような変数で表すと便利です。つまり、4次元配列のメモリーA(m,n,k,l)を準備しておき、積分結果をこの配列に入れます。
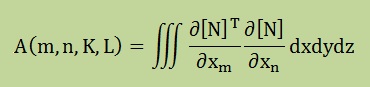
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |