次へ進む前に以下の定義をしておきます。
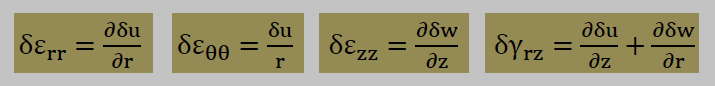
すると上の積分式Iは以下のように書けます。
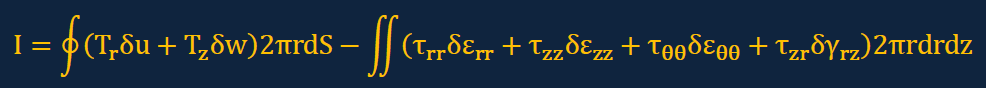
簡単な式になりました。1つ注目しておきたい点は、積分式Iを展開している過程で応力の内訳には一切触れていませんでした。しかし、上の式から言えることは、δεijの定義式のδを取り除くと、ひずみの定義であるεijとまったく同じになっています。
■軸対称円筒座標系の有限要素法■
上の理論的背景から必要な応力、ひずみ、変位および積分式Iの詳細がわかりました。有限要素法では、これらを関係づける式を作り、積分式Iを用い剛性マトリクスの代数式を導きだします。結果、連立方程式を解くことにより変位が得られ、それを元にひずみと応力が計算されます。
有限要素法では、まず、応力とひずみとの関係、ひずみと変位との関係をマトリクスで表します。そうすることにより、プログラミングが容易になってきます。まず、変位のuとwは、これまで通りu(r,z)=[N]{u}, w(r,z)=[N]{w}で書けます。[N]は要素の形状関数マトリクスです。ここでは、9節点2次要素を取り上げて話を進めたいと思います。すると、[N] マトリクスは以下のようになります。
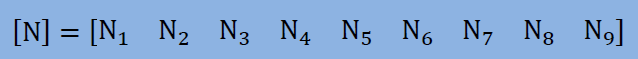
変位が定義できれば、ひずみも簡単に計算できます。下は、ひずみと変位の関係を表しています。
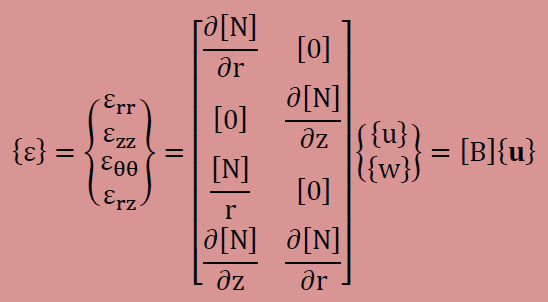
ここに、[B]マトリクスは以下のように定義できます。
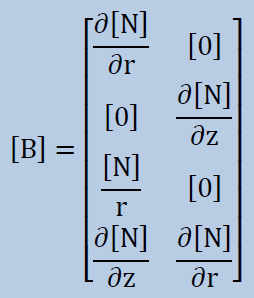
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |