■固有振動周波数の解析例:片持ち梁■
1次元で用いた例題を8節点1次ヘキサ要素と27節点2次ヘキサ要素で領域分割し、1次元の結果と比較してみましょう。再度、1次元の計算で用いた片持ち梁を下に示しておきます。
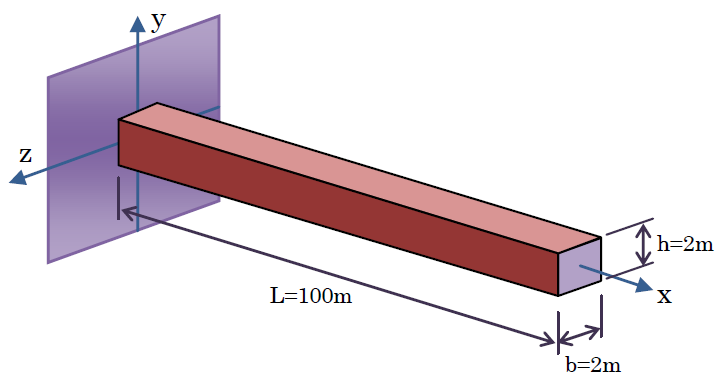
材料定数は、E=205GPa, ρ=7860Kg/m3でした。3次元ではポワソン比(ν)が必要になります。ここでは、ν=0.3を用いることにします。
■1次要素の解
要素分割ですが、下表に示すように様々なケースをトライし、精度を確認したいと思います。出来るだけ要素の形状を正立方体に保つようにx,y,z方向の要素分割を決めています。ただし、固有値の重根を避けるためにz方向の分割数をy方向より1つ多くしてあります。Jacobs法を使っているため重根は
気にする必要はありませんが、Bisection法やBisection/Newton-Raphson法でも問題なく計算出来るように、このような要素分割にしました。
| Case | x方向の分割数 | y方向の分割数 | z方向の分割数 |
|---|---|---|---|
| 1 | 100 | 2 | 3 |
| 2 | 200 | 4 | 5 |
| 3 | 300 | 6 | 7 |
| 4 | 400 | 8 | 9 |
| 5 | 500 | 10 | 11 |
境界条件ですが、x=0での変位 u, v, w を拘束する必要があります。計算結果を1次元と比較するわけですから、できるだけポワソン比(ν)の影響がでないような拘束にしなければなりませんが、とりあえず、x=0の全ての節点で u=0, v=0, w=0 を与えました。 入力データを作成するプログラムEIGENDATASET08.FORを実行し、その後固有値と固有ベクトルを計算するEIGENLANCZOS_SOLID3-JACOBS.FORを実行します。すると結果ファイルとして、SOLID-EIGEN-LANCZOS-JACOBS08.OUTを出力します。これはCase 1の計算結果です。また結果は表計算ソフトで読めるようにスペース区切りになっています。全てのCaseを計算しまとめると、以下の固有振動周波数(Hz)が得られました。
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |