つまり、これがLanczos法の特性ということです。また、この方法の特徴は、固有値の大きい順に現れてきます。 つまり、最小固有値はm=nにしないと現れてきません。しかし、設計で必要な固有値は、最小の値ですよね。 では、どうすればよいのか?。Lanczos法は、計算精度が高く計算が速いという素晴らしい特徴を持っています。 この特徴を生かしながら、最小の固有値が精度良く計算できる方法はないのか?。
この質問に答えてくれたのが、またまたLanczosなのです。彼の考えは、[A]{x}=λ{x}での固有値λを 固有振動数の逆数にすることでした。つまり、最小の固有振動周波数が最高精度の最大固有値になっているということです。 この場合、[A]の逆行列かまたは同等の計算が余分に必要になります。以下にその方法を詳細に紹介します。
その前に、例題で取り上げたn×nの[A]ような配列をした行列の固有値には、厳密解があります。それは、以下の式で得られます。
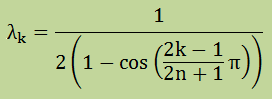
■Shifted-Invert Lanczos法■
この方法の特徴は、上でも言いましたが与えられた問題[A]{x}=λ{x}の固有値を逆数にすることです。
そして、計算上では固有値をShift parameterなるもので移動しておきます。
つまり、Shift parameter(δ)は、以下で定義します。
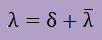
Shift parameter(δ)を行列[A]に反映させるために、行列[A]を以下のように変形します。
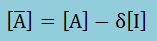
上の2式を[A]{x}=λ{x}に代入すると、以下が得られます。
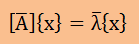
上式に前から[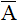 ]-1 を掛けると以下になります。
]-1 を掛けると以下になります。
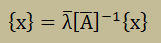
次に両辺を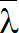 で割ります。すると、以下になります。
で割ります。すると、以下になります。
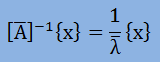
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |