■F(x,ξ) M1の積分■
それでは、早速、F(x,ξ) に形状関数 M1 を乗じた積分を行ってみましょう。下に、Gauss-Legendre 法で積分する方法を示します。和の内部は、全てηの関数になっていますので、直接計算できます。
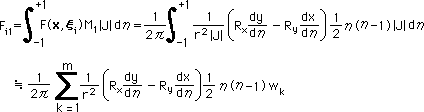
|
上の積分は、Source point の近くも、問題なく且つ精度良く計算できます。理由とし、上の積分には、R・n が含まれているため、Source point の近くでは、F(x,ξ) =0 になるからです。この件については、FREE TREM のセックッションで詳しく説明します。
■G(x,ξ) M1の積分■
次に、Kernel function の積分のやり方を説明します。下に、G(x,ξ) M1の積分を1例として示します。
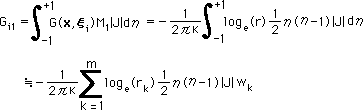
|
Kernel function の積分は、わりと簡単にプログラム出来ます。しかし、積分の精度が向上するように注意を払わないと、満足な結果は得られません。精度向上の一つとして、積分区間(-1,+1) を更に細分割する方法があります。もちろん、要素の長さを短くするのも、一つ方法ですが、これは、節点の数が多くなり、[A]{X}={RHS} のマトリックスのサイズも大きくなります。
| BACK | NEXT |
|---|
| Menu | Linear | Corner | Mixedform | Parabolic | Example |