■一定要素が角問題をもたない理由■
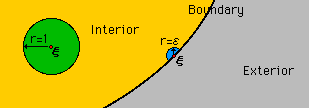
境界要素法のみ存在する問題が、Corner Problems(角問題) です。いったい、角問題とは、何なのか、なぜ起きるのかを、まず、紹介することにしましょう。
境界要素法の書物を読んでいると、smooth boundary (滑らかな境界) という言葉が、頻繁にでてきます。滑らかな境界上に点を落とし、C(ξ) を計算すると0.5 になります。つまり、下図に示す境界上の点での内角が、180度なっています。境界線上では、直線でも曲線でも、内角は180度ですからね。
さらに、境界要素法の書物をめくると、必ずと言っていいほど、Constant element (一定要素) のプログラムが紹介されています。そして、Source point は、下図に示す様に、一定要素の中央に位置しています。
 |
 |
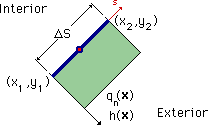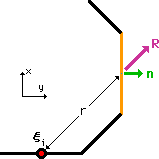
| この場合、Source point での内角は、常に180度になり、smooth boundary が保証されていることになります。また、一定要素上では、変数 h(s) と qn(s) は、一定になっています。つまり、Source point の前後で h(s) も qn(s) も連続になっています。 h(s)は、境界線上で連続であるのに対し、qn(s) はsmooth boundary以外において不連続になっています。qは連続なのですが、qの法線方向成分をとったqnは、smooth boundary以外で不連続になります。つまり、smooth boundary以外の節点では、2つの qnが存在することになります。しかし、未知数は１つのみですので、結果的に2つの qnの平均的な値が節点でのqnに入ることになります。これが、Corner Problems(角問題)なのです。この問題に対し、どうアタックすればよいかです。 |
| BACK to Linear Element | NEXT |
|---|
| Menu | Linear | Corner | Mixedform | Parabolic | Example |