境界条件についても、一定要素は、道理にかなっています。境界条件と境界値は、要素に与えます。離散化の過程で、どうしても境界条件は、節点に振り分けられます。したがって、境界要素法では、節点の境界条件が必要になります。つまり、節点で何が計算されるか(hi または qni) を知る必要があります。一定要素は、この辺が明確に定義されています。 一定要素の場合、節点が要素の中央にあるため、計算される変数 (hi または qni) がはっきりしています。例えば、hi が与えられていれば、 qni が計算されることになります。しかも、内角は常に180度です。誠に明白です。

一定要素がCorner problems を誘発しない理由が、理解できましたでしょうか。

■1次要素の場合はどうか■
1次要素には、下図に示す様に、要素の両端に節点が有ります。それらの節点は、他の要素の節点と共有されることになります。1次要素では、これらの節点でh_iと q_niが計算されます。

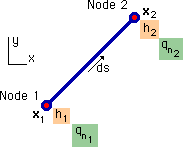
他の要素と共有されたとき、節点の内角は、必ずしも180度とは限りません。また、隣の要素の境界条件と同じとは、限りません。つまり、一定要素の利点が全部、御破算になってしまいます。つまり、計画の練り直しということになります。