■線形要素による積分式の離散化■
頭をリフレッシュするために、もう一度、Laplace 式を解く境界要素法の積分式を下に表示します。式中の index i は、Source point の番号です。

一定要素と同様に、ここでも、φ(x)=0 としました。
上式を線形要素(linear element) の形状関数とGauss-Legendre積分法の座標により離散化すると、次の様になります。ここまでは、問題なく理解できますよね。
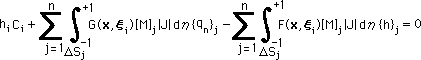 |
和の n は、要素の数です。Index i は、Source point が位置している節点番号を意味します。したがって、上式は、節点数と同数、存在することになります。線形要素で領域の境界を分割すると、節点数と要素数は、同じになります。これは、一定要素の時も同じでした。
話しを、離散化に戻しましょう。上式を線形要素の形状関数にしたがって展開すると、次の様になります。
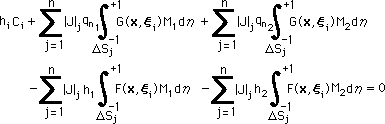 |
ここに、|J| は、一定要素の時と同じの、|J|=ΔS/2 です。ΔSは、要素の長さです。
ここも問題なく理解できますとね。未知数のhとqnを離散化しただけですから。
| BACK | NEXT |
|---|
| Menu | Linear | Corner | Mixedform | Parabolic | Example |