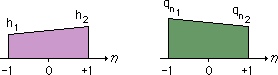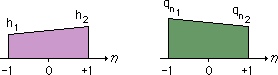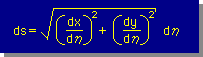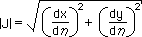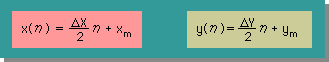■座標変換■
実座標系上の h(x) と q_n(x) (前のページ参照) を無次元座標系へ変換すると、下図の様に書けます。

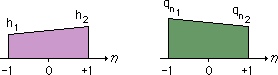変数 h と q_n は、xとy の関数でなく、無次元座標のηの関数になっています。このことは、実座標の xとy も無次元座標(η)の関数として書くことができます。つまり、実座標値と無次元座標値の変化を関係付ける全微分は、次の様に書けます。

そして、線積分の座標系(s)の変化とxy座標系との関係は、ds²=dx²+dy²ですから、線積分の座標系(s)の変化と無次元座標値の変化との関係は、下の様になります。

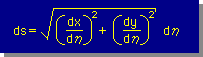上の式は、通常、ds = |J| dη で表します。ここに、|J|をJacobian matrix の Determinantといい、下式で表します。

また、1次要素において、 実座標の xとy と無次元座標のηを関係付ける式は、下式で表せられます。

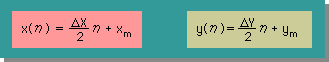ここまでは、一定要素(constant element) と全く同じです。復習のつもりで、再度、自分の力でこれまでに出てきた式を導いてみて下さい。