そして、Free term は、下式で計算できます。一定要素のFree term の計算方法も参考にして下さい。F(x,ξ)の積分を全部加算したのがCでしたよね。

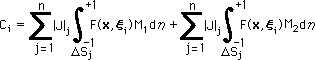これまでの積分式を観察すると、要素毎に下の4つの積分が必要になることが分かります。つまり、下の4つの積分が計算できると、1次要素を用いた境界要素法の積分式を完成させることができます。

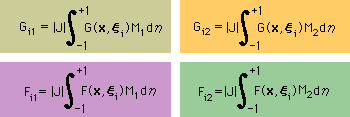
すると、境界要素法の基本式は、下の線形代数式で書けることになります。

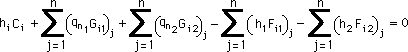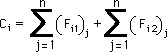ここでは、上の4つの積分をGauss-Legendre 積分法で計算する手順を紹介します。

次へ進む前に上式を簡単におさらいしておきます。 上の式で、j　は要素番号を示します。例えば、j=2の場合を取り上げます。要素1は節点番号1と2で、要素2は2と3で、要素3は3と4で構成されているとします。すると　j=2のq_n1は節点番号2でのq_nを意味します。また、j=1の場合、q_n2も節点番号2でのq_nを意味します。この辺を考慮しながらマトリックス[G]と[F]を作り上げてゆくことになります。詳細は、例題で説明しますので安心して下さい。ここでは、感覚を身に付けて頂けれOKです。