計算結果をSOLUTION.BEM-CORNER-2に示します。結果を見ると、あまり精度は改善されていないことに、気付くと思います。つまり、節点17でのq_n=0.3882 で 節点18でのq_n=0.4004 です。それぞれ0.7854と0に近い数値でなくてはなりません。

納得できない解がでてきました。なんとなく、境界要素法の限界を見た様な気がします。多分、このケースは、境界要素法にとってかなり不利な問題であることには間違いなさそうです。これでGive up するのは、まだ早いです。次の手を考えてみましょう。

■Corner 問題へのトライ: その2■
節点17と節点18の座標値を、ちょっとだけ元の位置から移動します。節点17の座標値を、(0,2) から (0.001,2) へ、そして、節点18の座標値を、(0,2) から (0,1.999) へ移動します。詳細は、入力データBEM2.DAT-CORNER-PROBLEMS-3を見て下さい。

計算結果は、SOLUTION.BEM-CORNER-3にあります。 結果を見ると、精度は下図に示す様に、かなり改善されています。節点17でのq_n=0.08605 で 節点18でのq_n=0.7399 です。節点18での厳密解は、q_n=0.7854 ですから、かなり良い線まで精度が上がって来ています。図中の()内の数値は、厳密解です。

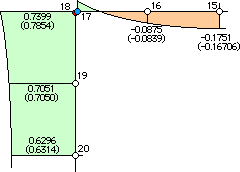
計算結果を見ると、温度 h(x,y) の精度が若干低下している様です。h(1,1)=0.26685 と h(2,1)=0.37725 となっています。多分、これらの誤差は、境界をopen にしたことによると考えられます。したがって、この様な境界条件と領域の形状の場合、q_nに振り回されない様に解析を進める方が、全体的に良い結果を生むことになりそうです。有限要素法で同じ問題を解析する場合、q_n を計算することはありませんからね。