前ページの解を、もう1回積分すると、s(u) が求まります。この時、積分範囲を決める必要が有ります。つまり、時間が 0 から t まで進んだ時、drawdown は、0 から s まで変化します。一方、変数 u は、∞から u まで変化することになります。
式で書くと次の様になります。

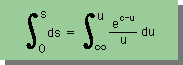
よって、s(u)は、下式の様に、中途半端な状態で示されています。もちろん、後程紹介する、無限級数でも表すことが出来ます。

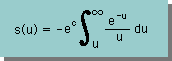
ここで、Well(井戸)の境界条件について補足説明しておきます。

Well から水を汲み出す量をQ_w で、そしてwellへ水を供給する量をQ_c で表すことにします。すると、半径rのwellからのQ_cは、Darcy's law より、次の様に書けます。

Q_wの場合、水の流れの方向と座標軸(r)の方向が、正反対ですから、Q_wは下式のように、マイナス符号が付きます。

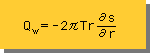
先ほど紹介した、境界条件は、上の式がベースになっています。

次に、その境界条件から、支配方程式の解の積分定数を導きます。