■λdivVの値について■
これまでの数式の展開とDriven-cavity の数値計算の結果から明確になったことは、下の2つです。
| 第2粘性係数が大きくなると、流体はより非圧縮性になる。つまり、divVは、1/λに比例する。 |
| λが無限大でもλdivVは、有限な値を持つ。 |
つまり、Navier-Stokes equations のλdivV=0の仮定は間違いで、そしてλ>0 でなくてはならないことは明白といえます。結果的に、非圧縮性の流体を解くために、通常の流体解析では、Navier-Stokes equations に連続の式を連立に解かなくてはならない羽目になっています。また、Navier-Stokes equations の中では、λdivVが事実上不在しているため、解析に矛盾が生じていることになります。その矛盾は、多分、平均圧力にしわ寄せされているはずです。
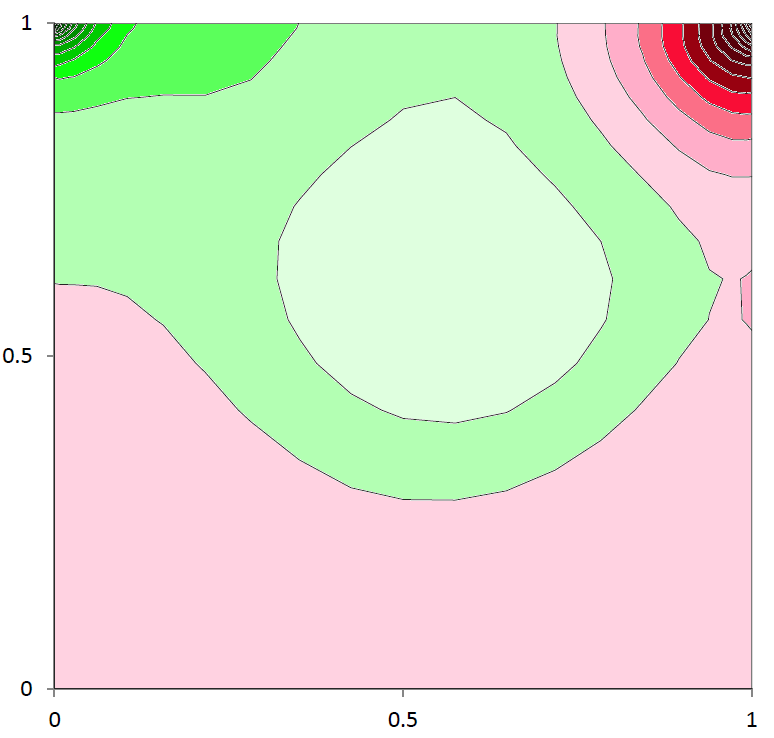
下図にR=400、λ/μ=1x107で計算した圧力分布(-λdivV)を示します。TMAX=400で計算しました。緑に近い色が引っ張りを、そして、赤に近き色が圧縮を表します。図を見ても、スムーズな圧力分布が描かれていることがわかります。
話しを、Navier-Stokes equations に戻します。先ほど、Navier-Stokes equations を非圧縮性の流体として解くのに連続の式が必要といいましたね。つまり、結果的に連続の式が流れを非圧縮性に保っていることになります。これは、私達が勝手に流体を非圧縮性にしていることになります。弾性解析では、Poisson's ratio が非圧縮性の度合を表してますが、流体では、非圧縮性に度合がなく、常に1種類の非圧縮性流体のみが存在しています。
自然界では、非圧縮性の流れになりうる流体として、空気、水、アルコール、油、水銀等がありますが、Navier-Stokes equations からの答えは、1種類になります。勿論、μの値は違いますがね。
| BACK | NEXT |
|---|
| Menu | Govern | FEM | 2nd Visco | DCF | Cylinder | /Heat | Lub |