下に、粘性係数比(μとλ)の値を1から1x10⁹まで変化させたときの、流れの移り変わりをアニメーションで表示しています。粘性係数比が1はどちらかと言うと空気で、粘性係数比が1x10⁹は水といったところですかね。

R=400, λ/μ=1 to 1x10⁹

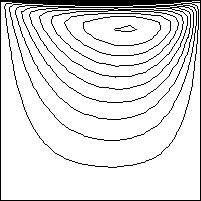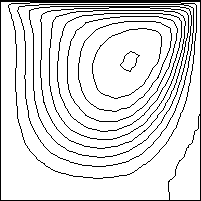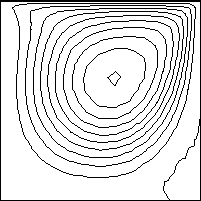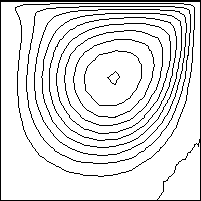
計算結果から分かったことは、 λ/μ=1x10⁷から1x10⁹の間の第2粘性係数を使った解析では、流れに大きな変化はみられなかったことです。つまり、このシステムでは、λ/μ=1x10⁷で、十分な非圧縮性流れが得られていることを意味しています。

さらに、詳しく第2粘性係数の役割を調査するために、divV と λdivV を1/λ でプロットすることにします。つまり、グラフの縦軸がdivV or λdivV で、横軸がμ/λ です。また、計算に用いたλは、指数で変化していますので、グラフの作成には、対数を用いました。下に、領域のほぼ中央部の要素でのdivV or λdivV の値がプロットされています。

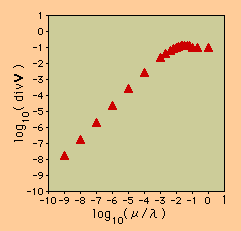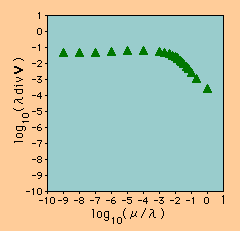divV vs. μ/λ	λdivV vs. μ/λ

結果を観察すると、divV は、λの値が大きくなるにつれ小さくなってきています。ほぼ、divV ∝1/λ の関係になっているのが確認できます。λdivV は、λの値が大きいところで、ほぼ一定値になっています。これらは、期待通りの結果ですね。