次はHeat equationです。Heat equation の両辺をρ0Cp0で割った式を下に示します。温度分布は、水の微量な密度や比熱の変化に左右されないということが前提になっています。
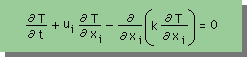
これで必要な式は、全て揃いました。次は、これをFEMで解く方法を紹介します。
■計算方法■
運動方程式とHeat equationがリンクされているのは、運動方程式のBody force termのみです。さらに、Body forceは、温度の2乗に比例していますので、両式を直接連立に解くことは出来ません。
そこで、ここでは、運動方程式とHeat equationは別々に解いて、速度分布と温度分布の収束性を、タイムステップ毎にチェックし、収束していると判断したら、次のタイムステップへ進むというアルゴリズムを採用しています。
このプログラムの作成で最も注意を要したことは、Heat equationの解法です。熱伝導率(単位がcm2/sec)は、Kinematic粘性係数の約 1/10 であるから、要素サイズが運動方程式の解法に問題がなくても、Heat equationの解析では、convective termsからの悪影響が解析結果に現われてきます。
したがって、Heat equationの離散化には、Upwind法を適用する必要が生じてきます。つまり、Added viscosityのことです。プログラムの中の変数(C1)がHeat equationの中のUpwind法を制御しています。C1=1. がUpwind法有りで、C1=0. が無しです。しかし、ここで使っているUpwind法は、線形要素用ですので、4-noded Iso-parametric 要素(このプログラムで使用)では、ちょっと不適切といえます。そこで、ここでの例題紹介では、C1=1.2 を使い不適切性をカバーしています。勿論、小さな要素を使えば、Upwind法の手助けは不要になります。
したがって、プログラムの大まかなアルゴリズムは、次の様になっています。
| 現時点(t)での温度分布(T)をt+Δt時の温度分布と仮定する。 |
| 現時点(t)での速度分布(U, V)をt+Δt時の速度分布と仮定する。 (Vは、重力加速度方向(180度方向)の流体の速度です。) |
| t時とt+Δt時の温度分布でt+Δt時のBody forceを計算する。 |
| t時とt+Δt時の速度分布とBody forceでt+Δt時の速度分布を計算する。 |
| Upwind法とt+Δt時の速度分布で、Added viscosityを計算する。 |
| t時とt+Δt時の速度分布と温度分布でt+Δt時の温度分布を計算する。 |
| t+Δt時の U, V, T と計算されたt+Δt時の U, V, T から誤差を計算する。 |
| 計算された t+Δt時のU, V, T をt+Δt時の U, V, T とする。 |
| 誤差が許容範囲内であれば、次のタイムステップへ進む。誤差が大きければ、上を繰り返す。 |
| 時間をΔt 進める。 |
| BACK | NEXT |
|---|
| Menu | Govern | FEM | 2nd Visco | DCF | Cylinder | /Heat | Lub |