前ページの最後の式は、通常、ds = |J| dη で表します。そして、|J|をJacobian matrix の Determinantといい、下式で表します。
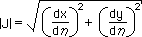 |
一定要素や1次要素において、2|J|は要素の長さでしたが、2次要素では、無次元座標(η)の関数になります。つまり、|J|=f(η) です。
■2次要素による積分式の離散化■
、頭をリフレッシュするために、もう一度、Laplace 式を解く境界要素法の積分式を下に表示します。

一定要素と同様に、ここでも、φ(x)=0 としてあります。
上式を2次要素 の形状関数とGauss-Legendre積分法の座標により離散化すると、次の様になります。
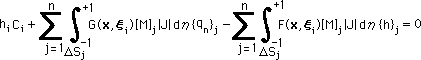 |
| BACK | NEXT |
|---|
| Menu | Linear | Corner | Mixedform | Parabolic | Example |