■座標変換■
2次要素での座標変換も一定要素や1次要素の時と、殆ど同じです。復習の意味も含めて、再度、説明します。今回は、まず、無次元座標系から実座標系への変換式を作ってみましょう。形状関数と節点での実座標の値(xiとyi) は、次の式で書けます。
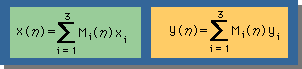
上の式を展開すると、次の様になります。
 |
次に、Gauss-Legendre積分法による数値積分を行うために、dsをdηへ変換する必要があります。このために、実座標のxとyの全微分を無次元座標の(η)で表す式が必要になります。式は、次の様になります。

そして、線積分の座標系(s)の変化とxy座標系との関係は、ds2=dx2+dy2ですから、線積分の座標系(s)の変化と無次元座標値の変化との関係は、下の様になります。これは、以前にも紹介しました。
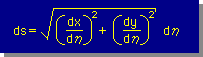
| BACK | NEXT |
|---|
| Menu | Linear | Corner | Mixedform | Parabolic | Example |