つまり、上流からやって来た流体の上半分は、ψ(x,y)=0 と ψ(x,y)=Ud の間を流れることになります。そして、領域内では、渦が発生しないという条件を流体に与えると、L(ψ(x,y))=0 が成り立ちます。つまり、Laplace 式を下の境界条件で解析すると、領域内の流速分布が得られることになります。 図中の v は、y軸方向の流速を意味します。
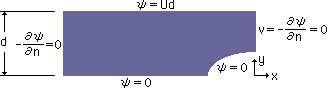
|
上図の左側面(-x面) の境界条件として、∂ψ/∂n=0 を与えていますが、代わりにψ=Uy を与えることができます。結果に多少の違いは有りますが、∂ψ/∂n=0 の方がψ=Uy に比べ、corner 問題を起こさないので良い結果が期待できます。左側面のψ=Uy については、計算結果で確認することにします。
数値解析を行う前に、ψ(x,y)=0 になる線を決めておく必要があります。つまり、ほぼ楕円柱のxとyの座標値です。この線を得る最も最適な方法として、Newton-Raphson 法があります。 ここでは、U=1, d=10, q=20, a=5 を用いて計算してみました。結果は、下表にまとめてあります。
| x座標 | y座標 | x座標 | y座標 |
|---|---|---|---|
| -7.171745 | 0. | -4.5 | 3.504899 |
| -7.0 | 1.02191 | -4.0 | 3.70818 |
| -6.8 | 1.48934 | -3.5 | 3.87289 |
| -6.6 | 1.82731 | -3.0 | 4.005888 |
| -6.4 | 2.09983 | -2.5 | 4.11208 |
| -6.2 | 2.33031 | -2.0 | 4.194759 |
| -6.0 | 2.53017 | -1.5 | 4.256721 |
| -5.8 | 2.70681 | -1.0 | 4.299732 |
| -5.6 | 2.86473 | -0.5 | 4.325062 |
| -5.4 | 3.00690 | 0.0 | 4.333239 |
| -5.2 | 3.13584 |
Stagnation point である、(-7.171745,0.) の点は、u(x,y)=∂ψ/∂y=0 より計算しました。
| BACK | NEXT |
|---|
| Menu | Linear | Corner | Mixedform | Parabolic | Example |