■両方の要素の境界条件が違う場合■
次に、Corner problems その2です。まず、問題は、何であるかを紹介する前に、この問題の対処法を先に伝えておきます。それは、連立方程式 [A]{X}={RHS} を直接、生成することです。つまり、離散化の過程で、[C]{h}+[G]{q}-[F]{h}={0} を暫定的に生成しないことです。昔の境界要素法の技術者が、この問題の対処法を発見したのは1970年代の後半から1980年代の前半にかけてです。それ以前は、[C]{h}+[G]{q}-[F]{h}={0} をベースに話しが進められていました。本や論文も多数、出版されています。ところが、[C]{h}+[G]{q}-[F]{h}={0} を使える条件は、smooth boundaryのみだったのです。この辺を理解していなかった技術者が1次要素に適用してしまったのです。これが問題の発端になっているのです。
ここでは、問題とは何か、[C]{h}+[G]{q}-[F]{h}={0} をベースにすると何故、問題を引き起こすのかを説明します。
まず、下図をみて下さい。節点 A を共有している両要素の境界条件が、互いに違います。この様な場合、節点 A の境界条件は、どの様に理解すれば良いのでしょう。

従来の離散化の方法では、節点 A の境界条件をDirichlet 型としています。確かにh(x,y) は、既知です。しかし、要素A-C の qn も既知です。”どうすれば良いのでしょう”と昔の技術者は考えました。彼等が考えた末の回答は、節点Aでの qn は、未知として取り扱うことにしました。まー、従来の離散化ですと自然にそうなるということです。
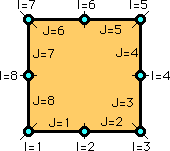
では、従来の離散化とは、どんな方法であったか数式を用いて説明します。従来の離散化とは、最初、[C]{h}+[G]{q}-[F]{h}={0} を生成します。それから、上で説明した節点での境界条件の選択方法を用い、連立方程式 [A]{X}={RHS} を作り上げます。説明のために、前に紹介した、下図の例題を使います。
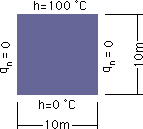 |
 |
|---|
| BACK | NEXT |
|---|
| Menu | Linear | Corner | Mixedform | Parabolic | Example |