■計算結果■
まず、input data を見て下さい。最後の2行に注目して下さい。数字の1は、point source の数を示します。そして、0. 0. 1000. は、それぞれ、point source の位置を示す x 座標値、y 座標値、それにpoint source のマグニチュードを示す Q1 です。Input ファイルの名前は、BEM2.DAT です。
計算結果は、ファイル名 SOLUTION.BEM に入ります。早速、結果のFluxをチェックしてみましょう。qn は、約16ですから、これに円周(2*π*10) を乗ずると全Flux は、1005 になります。Point souece のQ1=1000 ですから、満足のいく値になっていますね。誤差は。0.5%です。
次に、領域内の点について、解析精度を調べてみましょう。まず、例題の場合の厳密解は、下の様になります。
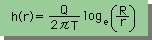
厳密解と解析値を下表にまとめてありますので、確認して下さい。表を見ると、荒っぽい要素分割でも、かなり良い結果を出しているのに気付くと思います。
| 半径 r | 厳密解 | 解析値 | 誤差(%) |
|---|---|---|---|
| 0 | ∞ | ||
| 2 | 256.15 | 255.67 | 0.19 |
| 4 | 145.83 | 145.34 | 0.34 |
| 6 | 81.30 | 80.790 | 0.63 |
| 8 | 35.51 | 34.980 | 1.49 |
| 10 | 0. | 0. | 0 |
次は、有限要素法でも紹介した Free surface の計算です。