すると、無次元の座標系で積分されるF'ij(x,ξ) は、下の様になります。
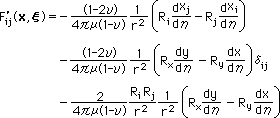 |
■関数 F'ij(x,ξ)■
上の関数をみると、Laplace 式のときよりかなり複雑になっています。しかし、δij の項は、Laplace 式と同じですから、この項については、極限をチェックする必要はありません。その他の項(第1項と第3項)についても、Laplace 式で得られた下の結果を活用することが出来ます。
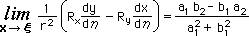 |
| BACK | NEXT |
|---|
| Menu | Laplace Equation | Taking Limits | Navier's Equation |