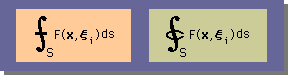
■疑問に感じる説明その1: C(ξ)■
境界要素法の論文や本を読むと、C(ξ) についての明解な説明がありません。また、あったとしても、下に示す様な積分記号を使って、あいまいな解説がなされているだけです。もちろん、数学において、この様な積分記号は有りません。

本によると、上式のF(x,ξ) は、r=0 近辺で、G(x,ξ) よりも特異性が強く、積分するには、不適切 (impoper) であるとしています。 つまり、C(ξ) は、直接、計算できないと述べています。 しかし、下の境界要素法の積分式は、全て適切な積分(問題なく積分できる)から構成されています。 つまり、C(ξ) 以外の全ての積分が適切であるなら、C(ξ) も適切な積分であることになります。

なぜ、書物には、上で述べたあいまいな積分記号で、あいまいな説明をしているのかを、私なりに考えてみました。 理由のその1つを下に述べます。

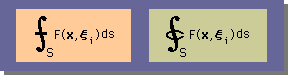
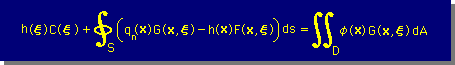
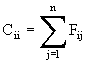前にも述べましたが、Laplace equation を境界要素法で解く場合、C(ξ) を計算することなく、未知の{q}と{h}を解くことができます。その方法とは、[C]{h}+[G]{q}-[F]{h}={0} を [G]{q}=[[F]-[C]]{h} と並び替え、{h}={1}と{q}={0}を適用するとCii は以下の式から求めることが可能になります。有限要素法でも2階微分項の特徴として紹介しました。 したがって、C(ξ) の値が分からなくても、事実上、問題はないわけです。つまり、C(ξ) について、あいまいな説明をしても、しなくても、差し支えないことになります。しかし、式を導く過程で、あいまいは、許されません。