もう1つの疑問に感じる説明は、以下のようになっています。これは、私に推測です。
| 境界要素法のベースを作り上げた人物は、G. Green です。彼は、Interior Equation を導き、境界上の h(x)とqn(x)が既知であれば、Interior のh(ξ) を直接的に計算できることを示しました。 しかし、彼は、 h(ξ) が境界上に位置しているときの式(Boundary Equation) は、導かなかったのです。したがって、彼の後、境界要素法に携わった人々は、Interior Equation から Boundary Equation を導くことを考えました。これは、まったくの間違った考えで、C(ξ) を無視したことによる誤解です。結果的に、C(ξ) は議論されず、間違った Boundary Equation の導き方が書物に書かれることになりました。 |
■関数 F(x,ξ) の特性■
では、早速、x が Source point 近傍のF(x,ξ) の特性について調べてみましょう。その前に、F(x,ξ) は、何だったかを復習してみましょう。
関数 F(x,ξ) は、下に示す Kernel function G(x,ξ) の微分でした。
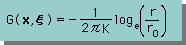
正確には、G(x,ξ) を境界線上で境界線に対し、放線方向に微分した関数です。下の左をみて下さい。 実際に微分すると、下の右の様になります。
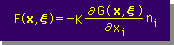 |
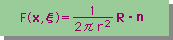 |
式中のR=Rxi+Ryj と r は、次の様に定義されていました。nは、unit normal vectorです。
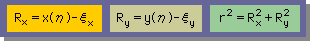
| BACK | NEXT |
|---|
| Menu | Laplace Equation | Taking Limits | Navier's Equation |